Howard Eves: «ΜΕΓΑΛΕΣ ΣΤΙΓΜΕΣ ΤΩΝ
ΜΑΘΗΜΑΤΙΚΩΝ»
 Η
ανακάλυψη των άρρητων αριθμών και των ασύμμετρων μεγεθών δημιούργησε τεράστιο
θόρυβο στις τάξεις των πυθαγορείων. Πρώτα απ' όλα φαινόταν να πλήττει
θανατηφόρα την πυθαγόρεια φιλοσοφία που υποστήριζε ότι όλα εξαρτώνται από τους
ακέραιους αριθμούς. Πώς είναι δυνατόν ένας άρρητος αριθμός όπως ο √2 να
εξαρτάται από τους ακέραιους αριθμούς, όταν δεν μπορεί να γραφτεί ως λόγος δυο
τέτοιων αριθμών; Έπειτα, φαινόταν αντίθετο με την κοινή λογική, που υποδείχνει
ότι κάθε μέγεθος μπορεί να εκφραστεί με κάποιο ρητό αριθμό. Το γεωμετρικό
αντίστοιχο ήταν εξίσου εντυπωσιακό, γιατί, πάλι σε αντίθεση με τη διαίσθηση,
διαπιστώθηκε ότι υπάρχουν ευθύγραμμα τμήματα που δεν έχουν κοινή μονάδα
μέτρησης. Όλη η πυθαγόρεια θεωρία της αναλογίας και των όμοιων σχημάτων ήταν
χτισμένη πάνω στη φαινομενικά προφανή υπόθεση ότι δύο οποιαδήποτε ευθύγραμμα
τμήματα είναι σύμμετρα, δηλαδή έχουν κάποια κοινή μονάδα μέτρησης. Ένα μεγάλο
μέρος της γεωμετρίας που οι πυθαγόρειοι θεωρούσαν ότι είχαν κατοχυρώσει έπρεπε
ξαφνικά να απορριφθεί σαν άχρηστο, αφού οι αποδείξεις ήταν λαθεμένες.
Προαγγελλόταν μια μεγάλη κρίση στα θεμέλια των μαθηματικών. Ήταν τόσο μεγάλο το
«λογικό σκάνδαλο» ώστε, σύμφωνα με τις φήμες, έγιναν για ένα διάστημα προσπάθειες
να κρατηθεί μυστικό το γεγονός. Ένας θρύλος λέει ότι ο πυθαγόρειος Ίππασος από
το Μεταπόντιο εξαφανίστηκε στη θάλασσα εξαιτίας της ασέβειας του να φανερώσει
το μυστικό στους ξένους, ή (σύμφωνα με μια άλλη εκδοχή) εξορίστηκε από την
κοινότητα των πυθαγορείων και στήθηκε ένα μνήμα του σαν να είχε πεθάνει.
Η
ανακάλυψη των άρρητων αριθμών και των ασύμμετρων μεγεθών δημιούργησε τεράστιο
θόρυβο στις τάξεις των πυθαγορείων. Πρώτα απ' όλα φαινόταν να πλήττει
θανατηφόρα την πυθαγόρεια φιλοσοφία που υποστήριζε ότι όλα εξαρτώνται από τους
ακέραιους αριθμούς. Πώς είναι δυνατόν ένας άρρητος αριθμός όπως ο √2 να
εξαρτάται από τους ακέραιους αριθμούς, όταν δεν μπορεί να γραφτεί ως λόγος δυο
τέτοιων αριθμών; Έπειτα, φαινόταν αντίθετο με την κοινή λογική, που υποδείχνει
ότι κάθε μέγεθος μπορεί να εκφραστεί με κάποιο ρητό αριθμό. Το γεωμετρικό
αντίστοιχο ήταν εξίσου εντυπωσιακό, γιατί, πάλι σε αντίθεση με τη διαίσθηση,
διαπιστώθηκε ότι υπάρχουν ευθύγραμμα τμήματα που δεν έχουν κοινή μονάδα
μέτρησης. Όλη η πυθαγόρεια θεωρία της αναλογίας και των όμοιων σχημάτων ήταν
χτισμένη πάνω στη φαινομενικά προφανή υπόθεση ότι δύο οποιαδήποτε ευθύγραμμα
τμήματα είναι σύμμετρα, δηλαδή έχουν κάποια κοινή μονάδα μέτρησης. Ένα μεγάλο
μέρος της γεωμετρίας που οι πυθαγόρειοι θεωρούσαν ότι είχαν κατοχυρώσει έπρεπε
ξαφνικά να απορριφθεί σαν άχρηστο, αφού οι αποδείξεις ήταν λαθεμένες.
Προαγγελλόταν μια μεγάλη κρίση στα θεμέλια των μαθηματικών. Ήταν τόσο μεγάλο το
«λογικό σκάνδαλο» ώστε, σύμφωνα με τις φήμες, έγιναν για ένα διάστημα προσπάθειες
να κρατηθεί μυστικό το γεγονός. Ένας θρύλος λέει ότι ο πυθαγόρειος Ίππασος από
το Μεταπόντιο εξαφανίστηκε στη θάλασσα εξαιτίας της ασέβειας του να φανερώσει
το μυστικό στους ξένους, ή (σύμφωνα με μια άλλη εκδοχή) εξορίστηκε από την
κοινότητα των πυθαγορείων και στήθηκε ένα μνήμα του σαν να είχε πεθάνει.
Ας δούμε τώρα μέσα από ένα παράδειγμα με
ποιον τρόπο οι αρχαίοι πυθαγόρειοι πίστευαν ότι είχαν αποδείξει μια βασική πρόταση
σχετικά με τα εμβαδά τριγώνων.
ΘΕΩΡΗΜΑ:
Τα εμβαδά δύο τριγώνων που έχουν το ίδιο ύφος έχουν τον ίδιo λόγο που έχουν και
οι βάσεις τους.
Αρχαία πυθαγόρεια απόδειζη: Έστω ΑΒΓ και ΑΔΕ τα δύο τρίγωνα και ΒΓ και ΔΕ οι
βάσεις τους που βρίσκονται στην ίδια ευθεία γραμμή ΜΝ, όπως στο σχήμα 21.
Θέλουμε να αποδείξουμε ότι:
Ετριγ. (ΑΒΓ): Ετριγ(ΑΔΕ) =
ΒΓ:ΔΕ.
Έστω (σύμφωνα με την πεποίθηση των αρχαίων
πυθαγορείων ότι δύο οποιαδήποτε ευθύγραμμα τμήματα είναι σύμμετρα) ότι κάποια
κοινή μονάδα μέτρησης των ΒΓ και ΔΕ περιέχεται p φορές στο ΒΓ
και q φορές στο ΔΕ. Σημειώνουμε αυτά τα σημεία διαίρεσης του ΒΓ και του ΔΕ και
τα συνδέουμε με την κορυφή Α. Τότε τα τρίγωνα ΑΒΓ και ΑΔΕ διαιρούνται
αντίστοιχα σε p και q μικρότερα τρίγωνα, που όλα έχουν το ίδιο ύψος
και ίσες βάσεις και συνεπώς, (Ετριγ.= ½ βάση επί ύψος) έχουν και το ίδιο εμβαδόν.
Άρα:
Ετριγ (ΑΒΓ): Ετριγ (ΑΔΕ) = p:q =
ΒΓ:ΔΕ
και η πρόταση αποδεικνύεται.
Η ανακάλυψη που έγινε αργότερα ότι δύο
ευθύγραμμα τμήματα δεν είναι πάντα σύμμετρα έκανε την απόδειξη αυτή όπως και
άλλες, ανεπαρκή και το συνταρακτικό «λογικό σκάνδαλο» πήρε σάρκα και οστά.
Αυτό το «λογικό σκάνδαλο» υπήρξε η πρώτη
γνωστή κρίση στα θεμέλια των μαθηματικών και δεν ξεπεράστηκε ούτε εύκολα ούτε
γρήγορα. Τελικά, γύρω στα 370 π.Χ. ο εξαίρετος έλληνας μαθηματικός Εύδοξος,
μαθητής του Πλάτωνα και του χαρισματικού πυθαγόρειου Αρχύτα, έδωσε μια λύση στο
σκάνδαλο με έξυπνο τρόπο, δίνοντας έναν ορισμό της αναλογίας, ή της ισότητας
δυο λόγων, εντελώς ανεξάρτητο από το αν τα μεγέθη που λάμβαναν μέρος σ' αυτή
ήταν σύμμετρα ή ασύμμετρα. Ο ορισμός αυτός που σημαδεύει μια μεγάλη στιγμή των
μαθηματικών είναι ο εξής:
Μεγέθη λέγονται ότι έχουν τον ίδιο λόγο το πρώτο προς
το δεύτερο και το τρίτο προς το τέταρτο, όταν τα ισάκις πολλαπλάσια του πρώτου
και τρίτου των ισάκις πολλαπλασίων του δευτέρου και τετάρτου καθ' οιονδήποτε
πολλαπλασιασμόν ή είναι μεγαλύτερα ή ίσα ή μικρότερα, όταν ληφθούν καταλλήλως[1].
Αυτός ο φλύαρος ορισμός, που φαίνεται
περισσότερο πολύπλοκος απ' ό,τι πραγματικά είναι, απλά εννοεί ότι αν Α, Β, Γ,
Δ, είναι τέσσερα μη προσημασμένα μεγέθη, από τα οποία τα Α και Β είναι του
ίδιου είδους (ευθύγραμμα τμήματα ή γωνίες ή εμβαδά ή όγκοι) και τα Γ και Δ
είναι του ίδιου είδους, τότε ο λόγος του Α προς το Β είναι ίσος με το λόγο του
Γ προς το Δ αν για τυχαίους θετικούς ακέραιους αριθμούς μ και ν, τότε:
Ας αποδείξουμε τώρα πάλι την πρόταση που είδαμε παραπάνω χρησιμοποιώντας αυτή τη φορά τον ορισμό της αναλογίας του Ευδόξου.
ΘΕΩΡΗΜΑ: Τα εμβαδά δύο τριγώνων που έχουν το ίδιο ύφος
έχουν την ίδιοι σχέση που έχουν και οι βάσεις τους.
Απόδειξη κατά τον Ευδοξο: Πάνω στην ευθεία ΓΒ (βλ. σχήμα 22) παίρνουμε μ-1
διαδοχικά ευθύγραμμα τμήματα από το μέρος του Β και ίσα με ΓΒ. Συνδέουμε τα
σημεία της διαίρεσης, Β2, Β3, ..., Βμ με την
κορυφή Α. Με τον ίδιο τρόπο, πάνω στην ευθεία ΔΕ παίρνουμε ν-1 διαδοχικά
ευθύγραμμα τμήματα από το μέρος του Ε και ίσα με ΔΕ και συνδέουμε τα σημεία της
διαίρεσης Ε2, E3, ...., Εν με την κορυφή Α.
Τότε:
ΒμΓ = μ(ΒΓ), Ετριγ.(ΑΒμΓ)
= μΕτριγ(ΑΒΓ)
ΔΕν = ν(ΔΕ) , ΕτριγΑΔΕν
= νΕτριγ(ΑΔΕ)
Από προηγούμενα αποτελέσματα έχουμε επίσης:
δηλαδή:
οπότε (από τον ορισμό της αναλογίας του Ευδόξου)
Ε(ΑΒΓ): Ε(ΑΔΕ) = ΒΓ:ΔΕ,
και η πρόταση αποδεικνύεται.
Στην παραπάνω απόδειξη δεν έγινε καμία
αναφορά σε σύμμετρες ή ασύμμετρες ποσότητες, αφού ο ορισμός του Ευδόξου ισχύει
εξίσου και στις δύο περιπτώσεις. Το «λογικό σκάνδαλο» που προέκυπτε από την
αντιμετώπιση των αρχαίων πυθαγορείων είχε επιδέξια ξεπεραστεί.
Μια κομψή παρουσίαση της θεωρίας της
αναλογίας του Ευδόξου έγινε αργότερα, γύρω στα 300 π.Χ., από τον Ευκλείδη στο
βιβλίο V των περίφημων Στοιχείων του. Ο Μπ. Μπολτσάνο (Ber-nhard Bolzano,
1781-1848), που υπήρξε ένας κατατρεγμένος τσεχοσλοβάκος ιερέας και
παραμελημένος μαθηματικός, έχει πει ένα διασκεδαστικό ανέκδοτο για τον εαυτό
του, στο οποίο ο Ευκλείδης και το Βιβλίο V των Στοιχείων του, έπαιξαν το ρόλο
του γιατρού. Ο Μπολτζάνο βρισκόταν σε διακοπές στην Πράγα, όταν προσβλήθηκε από
μια αρρώστια που εκδηλώθηκε με ρίγη και έντονες κοπώσεις. Για να μη σκέφτεται
την κατάσταση του, πήρε τα Στοιχεία του Ευκλείδη και διάβασε για πρώτη φορά τη
συναρπαστική παρουσίαση της θεωρίας του Ευδόξου για το λόγο και την αναλογία,
που ήταν στο Βιβλίο V. Η ευστροφία με την οποία αντιμετωπίζονταν τα θέματα τον
γέμισε με τόση πραγματική χαρά ώστε, όπως είπε, ανάρρωσε τελείως από την
αρρώστια του. Αργότερα, όταν κάποιος από τους φίλους του αισθανόταν κάποια
αδιαθεσία, του συνιστούσε σαν θεραπεία την ανάγνωση της παρουσίασης του
Ευκλείδη σχετικά με τη θεωρία του Ευδόξου.
Οι παιδαγωγικές δυσκολίες, που είναι
έμφυτες στην ασύμμετρη περίπτωση ορισμένων προτάσεων της γεωμετρίας του
επιπέδου και του χώρου, είναι αισθητές στις μέρες μας. Οι συγγραφείς πολλών
σχολικών βιβλίων, θεωρώντας ότι η θεωρία του Ευδόξου είναι ιδιαίτερα αφηρημένη
για αρχάριους μαθητές, προτείνουν αποδείξεις που χωρίζονται σε δύο περιπτώσεις,
τη σύμμετρη και την ασύμμετρη. Η σύμμετρη περίπτωση αντιμετωπίζεται με τρόπο
όμοιο με των αρχαίων πυθαγορείων, ενώ στην ασύμμετρη περίπτωση χρησιμοποιούνται
απλές έννοιες ορίων. Μερικές φορές η ασύμμετρη περίπτωση υποβιβαζόταν σ' ένα
παράρτημα για να καλυφθεί ανάλογα με τις διαθέσεις του διδάσκοντα, και άλλες
φορές παραλειπόταν τελείως σαν να ήταν έξω από τους σκοπούς του μαθήματος. Στα
περισσότερα σύγχρονα βιβλία γεωμετρίας η ασύμμετρη περίπτωση λαμβάνεται υπόψη
κάτω από ορισμένες προϋποθέσεις, όπως η γνώση της πληρότητας του συστήματος των
πραγματικών αριθμών και των βασικών του ιδιοτήτων.
Ας επιστρέψουμε τώρα στην πρόταση που
είδαμε παραπάνω για να μελετήσουμε την ασύμμετρη περίπτωση με τη βοήθεια κάποιων
απλών εννοιών των ορίων. Συγκεκριμένα θα χρειαστούμε το παρακάτω βασικό θεώρημα
της θεωρίας των ορίων, που εύκολα γίνεται κατανοητό.
ΘΕΜΕΛΙΩΔΕΣ ΘΕΩΡΗΜΑ ΤΩΝ ΟΡΙΩΝ. Αν δύο μεταβλητές είναι
πάντα ίσες και καθεμιά τείνει σε ένα όριο, τότε τα όρια αυτά είναι ίσα.
Ας δούμε τώρα την ενοχλητική ασύμμετρη περίπτωση.
ΘΕΩΡΗΜΑ: Τα εμβαδά δύο τριγώνων που έχουν το ίδιο ύφος
έχουν την ίδια σχέση που έχουν και οι βάσεις τους.
Ασύμμετρη περίπτωση: Ας υποθέσουμε ότι τα ΒΓ και ΔΕ στο Σχήμα 23 είναι ασύμμετρα. Θέλουμε
να δείξουμε ότι
ΔΑΒΓ: ΔΑΔΕ = ΒΓ:ΔΕ.
Διαιρούμε το ΒΓ σε ν ίσα μέρη, ώστε το ΒΖ να είναι ένα
από αυτά. Πάνω στο ΔΕ παίρνουμε διαδοχικά τμήματα ίσα με ΒΖ, φτάνοντας τελικά
σ' ένα σημείο Θ του ΔΕ τέτοιο ώστε ΘΕ<ΒΖ. Από τη σύμμετρη περίπτωση (που
θεωρούμε ότι έχει ήδη αποδειχτεί σύμφωνα με την πυθαγόρεια μέθοδο), έχουμε
Ετριγ(ΑΒΓ): Ετριγ(ΑΔΘ)
= ΒΓ:ΔΘ.
 |
Έστω τώρα ότι ν→∞. Τότε ΔΘ → ΔΕ και το Ετριγ(ΑΔΘ)
→ Ετριγ(ΑΔΕ), οπότε Ετριγ(ΑΒΓ)/Ετριγ(ΑΔΘ)
→ Ετριγ(ΑΒΓ)/ Ετριγ(ΑΔΕ) και ΒΓ/ΔΘ → ΒΓ/ΔΕ.
Το θεμελιώδες θεώρημα των ορίων συνεπάγεται τώρα:
Ετριγ(ΑΒΓ): Ετριγ(ΑΔΕ) = ΒΓ:ΔΕ
και έτσι αποδεικνύεται η ασύμμετρη περίπτωση.
Η παραπάνω προσέγγιση χρησιμοποιεί το
γεγονός ότι κάθε άρρητος αριθμός μπορεί να θεωρηθεί ως το όριο μιας ακολουθίας
ρητών αριθμών, προσέγγιση που αναπτύχθηκε με αυστηρό τρόπο πρόσφατα από τον
Κάντορ (1845-1918).
Υπάρχουν πολλοί λόγοι που συνιστούν να
συμπεριλαμβάνεται στην αποδεικτική γεωμετρία της μέσης εκπαίδευσης η απλή αυτή
διαδικασία με τα όρια που περιγράφτηκε παραπάνω. Γιατί, πρώτα απ' όλα, η έννοια
του ορίου απαιτεί αρκετό χρόνο για αφομοίωση και όσο πιο γρήγορα και πιο συχνά
αντιμετωπίζει ο μαθητής αυτή την έννοια τόσο το καλύτερο. Έπειτα, η θεωρία των
ορίων είναι βασική σε κάθε γεωμετρική μελέτη εμβαδών και όγκων. Τέλος, η
συζήτηση των ορίων στη μέση εκπαίδευση οπλίζει το μαθητή, αφού τον προετοιμάζει
ν' αντιμετωπίσει αργότερα την ανάλυση. Αν και υπάρχουν αξιωματικές προσεγγίσεις
στα πρώτα βήματα της γεωμετρίας που παρακάμπτουν την ανάγκη διάκρισης των
σύμμετρων και των ασύμμετρων περιπτώσεων, η θεωρία των ορίων είναι απαραίτητη
σε άλλα σημεία της γεωμετρίας. Συγκεκριμένα, καθώς προχωρούμε στη γεωμετρία
ανακαλύπτουμε ότι υπάρχουν πολλές έννοιες που ο ορισμός τους απαιτεί την ιδέα
του ορίου — όπως είναι το μήκος ενός καμπυλόγραμμου τόξου και η εφαπτόμενη
γραμμή μιας καμπύλης σ' ένα σημείο της καμπύλης.
Σε μια επόμενη μεγάλη στιγμή των
μαθηματικών θα δούμε με ποιον τρόπο διάφορα γεγονότα στις μέρες μας έχουν
δικαιώσει, τουλάχιστον όσο αφορά τα μαθηματικά, την πυθαγόρεια φιλοσοφία, ότι
όλα εξαρτώνται από τους φυσικούς αριθμούς. Θα δούμε επίσης ότι μια από τις
σύγχρονες μεθόδους πλήρωσης του συστήματος των πραγματικών αριθμών είναι με τη
βοήθεια της λεγόμενης τομής του Ντέντεκιντ (Dedekind), που είναι ουσιαστικά μια
αριθμητοποιημένη εκδοχή της θεωρίας του Ευδόξου για το λόγο και την αναλογία.
Ασκήσεις
6.1 Ας πάρουμε την πρόταση: Οι επίκεντρες γωνίες του
ίδιου κύκλου ή ίσων κύκλων έχουν την ίδια σχέση που έχουν και τα τόξα στα οποία
βαίνουν.
(α) Αποδείξτε, με την πυθαγόρεια μέθοδο, την πρόταση
όταν οι δυο γωνίες είναι ασύμμετρες.
(β) Αποδείξτε και τη σύμμετρη και την ασύμμετρη
περίπτωση με την μέθοδο του Ευδόξου.
(γ) Αποδείξτε την ασύμμετρη περίπτωση με απλές έννοιες
ορίων.
6.2 (α) Αποδείξτε, με την πυθαγόρεια μέθοδο και χρήση
ορίων, ότι: Μία ευθεία παράλληλη προς τη βάση τριγώνου τέμνει τις δύο άλλες
πλευρές σε μέρη ανάλογα.
(β) Αποδείξτε την πρόταση αυτή με τη βοήθεια του
θεωρήματος που αποδείχτηκε στη διάλεξη.
6.3 Αποδείξτε με την πυθαγόρεια μέθοδο και τη χρήση
ορίων ότι:
(α) Τα εμβαδά δύο ορθογώνιων παραλληλογράμμων με ίσα
ύφη έχουν λόγο όσο οι βάσεις τους.
(β) Δύο διεδρικές γωνίες έχουν λόγο όσο οι επίπεδες
γωνίες τους.
(γ) Οι όγκοι δυο ορθογωνίων παραλληλεπιπέδων με ίσες
βάσεις έχουν λόγο όσο τα ύφη τους.
6.4 Υπάρχουν τρία χαρακτηριστικά στην έννοια του ορίου
τα οποία πρέπει να σημειώσουμε προσεχτικά. Αν κ είναι το όριο μιας πραγματικής
μεταβλητής χ, τότε: (1) το κ είναι σταθερό, (2) η αριθμητική διαφορά ανάμεσα
στο χ και το κ γίνεται τελικά μικρότερη από οποιαδήποτε θετική ποσότητα ε, όσο
μικρή και αν επιλεγεί, (3) η αριθμητική διαφορά ανάμεσα στο χ και το κ παραμένει
τελικά μικρότερη από την ποσότητα ε.
Έστω ότι τα Α, Β και Γ, τρία συγγραμικά σημεία με το Β
ανάμεσα στα Α και Γ, παριστάνουν τρείς σταθμούς μιας ευθείας σιδηροδρομικής
γραμμής και έστω χ η απόσταση από το Α ενός τρένου Τ που ταξιδεύει προς το Γ.
Λαμβάνοντας υπόψη σας τα τρία χαρακτηριστικά του ορίου που περιγράψαμε πιο
πάνω, απαντήστε στις παρακάτω ερωτήσεις:
(α) Αν το τρένο Τ ξεκινά από το Α με σκοπό να
συνεχίζει να κινείται μέχρι να φτάσει στο Γ, είναι σωστό να πούμε ότι lim x =
ΑΒ;
(β) Αν το τρένο ξεκινά από το Α με σκοπό να συνεχίζει
να κινείται
μέχρι το Β, είναι σωστό να πούμε ότι lim x =ΑΓ;
(γ) Υποθέτουμε ότι μια εμπορική αμαξοστοιχία Σ
ταξιδεύει από το Α στο Γ και συμβολίζουμε με y την απόσταση της από το Α.
Υποθέτουμε ακόμα ότι το τρένο Τ κινείται πάνω σε μια παράλληλη τροχιά και
φεύγει από το σημείο Α λίγο μετά από τη Σ, φτάνει τη Σ και στη συνέχεια
ταξιδεύει παράλληλα με αυτό και με την ίδια ταχύτητα. Είναι σωστό να πούμε ότι
lim x = γ;
(δ) Αν το τρένο Τ ξεκινά από το Α και ταξιδεύει με
σταθερή ταχύτητα μέχρι που φτάνει στο τέρμα του Γ, είναι σωστό να πούμε ότι
lim x = ΑΓ;
(ε) Υποθέτουμε ότι το τρένο Τ ξεκινά από το Α και
ταξιδεύει προς το Γ με συνεχώς επιβραδυνόμενη ταχύτητα, έτσι ώστε σε 1
ώρα να έχει διανύσει το μισό της απόστασης ΑΓ, την
επόμενη ώρα να έχει διανύσει το μισό της υπόλοιπης απόστασης, την επόμενη πάλι
το μισό της απόστασης που έμεινε αυτή τη φορά κ.ο.κ. Είναι σωστό να πούμε ότι
lim x = ΑΓ;
6.5(α) Αν γνωρίζουμε πως μετράμε τα μήκη ευθυγράμμων
τμημάτων, πώς μπορούμε να ορίσουμε το μήκος της περιφέρειας ενός κύκλου;
(β) Αν γνωρίζουμε πώς μετράμε τα εμβαδά πολυγώνων, πώς
μπορούμε να ορίσουμε το εμβαδόν ενός κύκλου;
6.6 Έστω Πν και Εν η περίμετρος
και το εμβαδόν, αντίστοιχα, κανονικού ν-γωνου περιγεγραμμένου σε κύκλο διαμέτρου
μίας μονάδας. Να βρεθούν τα όρια limΠv και limEv.
6.7 Να διατυπώσετε ορισμό, κάνοντας χρήση ορίων, (α)
της εφαπτομένης καμπύλης σε ένα σημείο της.
(β) του εφαπτόμενου επιπέδου μιας επιφάνειας σε ένα
σημείο της.
6.8 (α) Αν γνωρίζουμε ότι ο όγκος μίας πυραμίδας είναι
ίσος με το ένα τρίτο του εμβαδού της βάσης της επί το ύφος της, πώς μπορούμε,
χρησιμοποιώντας έννοιες ορίων, να υπολογίσουμε τον τύπο που δίνει τον όγκο ενός
κυκλικού κώνου;
(β) Αν γνωρίζουμε ότι η παράπλευρη επιφάνεια ενός
κανονικού πρίσματος ισούται με την περίμετρο της βάσης του επί το ύφος του, πώς
μπορούμε να ορίσουμε την παράπλευρη επιφάνεια ενός ορθού κυκλικού κυλίνδρου;
Ίσως κάποιος σκεφτεί ότι θα μπορούσε να ορίσει το
εμβαδόν της παράπλευρης επιφάνειας ενός ορθού κυκλικού κυλίνδρου ως το όριο των
εμβαδών οποιασδήποτε ακολουθίας εγγεγραμμένων πολυεδρικών επιφανειών, όταν ο
αριθμός των εδρών των πολυεδρικών επιφανειών αυξάνεται απεριόριστα και το
εμβαδόν της μέγιστης έδρας τείνει στο μηδέν. Οι μαθηματικοί έμειναν έκπληκτοι
όταν στις αρχές της δεκαετίας του 1860, ο Σβαρτς (Η.Α. Schwarz, 1843-1921)
απέδειξε ότι αυτό δεν είναι σωστό.
Το παράδειγμα του Σβάρτς ήταν τόσο εκπληκτικό για τους
μαθηματικούς της εποχής, ώστε έγινε γνωστό ως παράδοξο του Σβάρτς.
Λύσεις
6.4.
(α) Όχι, η συνθήκη (3) δεν ισχύει,
(β)
Όχι, η συνθήκη (2) 8εν ισχύει,
(γ)
Όχι, η συνθήκη (1) 8εν ισχύει.
(8)
Ναι.
(ε)
Ναι.
6.5. (α) Έστω αν η περίμετρος ενός κανονικού
ν-γώνου εγγεγραμμένου στον κύκλο. Ορίστε την περιφέρεια γ του κύκλου ως
(β) Έστω αν το εμβαδόν ενός κανονικού ν-γώνου εγγεγραμμένου στον κύκλο. Ορίστε το εμβαδόν Α του κύκλου ως
Σχετική Βιβλιογραφία
1. Heath T.L., History of Greek Mathematics, 2 τομ., New York: Oxford University Press, 1931.
2. Zames, Frieda, "Surface area and the cylinder area
paradox", two-year College Mathematics Journal, Sept. 1977, σ. 205-211.




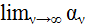
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου