Κλαύδιος Πτολεμαίος. G.LORIA.

G.LORIA. Ιστορία των Μαθηματικών.

Τα έργα του Αυτόλυκου, του Ευκλείδου, του Υψικλέους και του Αριστάρχου μαζί με άλλα μικροτέρας σημα­σίας, απετέλουν μέρος — κατά μαρτυρίαν του Αυτολύκου — της Μικράς Αστρονομικής Συντάξεως, η οποία περιελάμβανε τα απαραί­τητα έργα διά την κατανόησιν του μεγίστου αστρονομικού κωδικός, πού μας εκληροδότησεν η αρχαιότης. Εννοούμεν το διάσημον έργον του Κλαυ­δίου Πτολεμαίου, το όποιον αρχικώς έφερε τον τίτλον Μαθηματική Σύνταξις, ωνομάσθη δε - κατόπιν - υπό των μεταγενεστέρων θαυμαστών Μεγάλη Σύνταξις. Οι Άραβες, οι οποίοι μετέφρασαν το έργον εις την γλώσσαν των κατά τον VIII αιώνα, ήνωσαν το αραβικόν άρθρον αλ με την εξαραβισθείσαν προφοράν μαγέστα (αντί μεγίστη), και ούτω συνέθεσαν την λέξιν Αλμαγέστα, η οποία και παρέμεινεν έκτοτε γνωστή ως τίτλος του έργου. Η μελέτη του έργου τούτου είναι αναπόφευκτος δι' εκείνον, ο όποιος επιθυμεί να γνωρίση την αρχαίαν επιστήμην, αφού πρόκειται περί μιας εργασίας, χάρις εις την οποίαν ο Πτολεμαίος διετήρησεν επί πολλούς αιώνας αδιαφιλονίκητον κυριαρχικήν επιρροήν εις τα πνεύματα όλων των αστρονόμων.

Το ιστορικόν ενδιαφέρον του έργου απορρέει κατά πρώτον λόγον εκ του γεγονότος, ότι εξ αυτού αρυόμεθα τας πολυτιμοτέρας πληροφορίας γύρω από τον πρίγκηπα των Ελλήνων αστρονόμων, τον Ίππαρχον τον εκ Νικαίας (της Βιθυνίας)⁽¹⁾, όστις εισήγαγεν εις την Ελλάδα την διαίρεσιν τού κύκλου εις 360 μοίρας και έκαμε κατά τον ΙΙ αιώνα π.Χ. πολλάς παρα­τηρήσεις εις Ρόδον και Αλεξάνδρειαν, τοιαύτης σπουδαιότητος, ώστε — ως έγραφεν ο Πλίνιος —ήρθη εις στάθμην ανωτέραν της ανθρωπίνης, διότι έφερεν εις πέρας πράγματα, τα όποια μόνον οι θεοί θα ηδύναντο μετά κόπου να επιτελέσουν.

Ο δεύτερος λόγος, διά τον όποιον η μελέτη της Αλμαγέστας κατέχει ιδιαιτέραν ιστορικήν σπουδαιότητα, είναι διότι εις αυτήν ευρί­σκονται αι μοναδικαί και ασφαλείς βιογραφικαί πληροφορίαι γύρω από τον συγγραφέα της (διότι αι πληροφορίαι τας οποίας αφθόνως και λεπτο­μερώς παρέχουν οι Άραβες δεν είναι εν γένει αξιόπιστοι, λόγω τής επιδρά­σεως πολύ ζωηράς φαντασίας). Ατυχώς το σύνολον των δεδομένων ανάγε­ται τελικώς εις την πληροφορίαν ότι ο Πτολεμαίος έζησε περί το 150 μ.Χ.

Κατ' αναλογίαν προς τα Στοιχεία του Ευκλείδου και τα Αριθμητικά του Διοφάντου, η Μαθηματική Σύνταξις (Αλμαγέστα) διαιρείται εις 13 βιβλία. Το Βιβλίον Ι περιλαμβάνει τας προκαταρκτικός γνώσεις που είναι απαραίτητοι διά μίαν καρποφόρον έρευναν των ουρανίων φαινομένων, με βάσιν την υπόθεσιν ότι η Γη κατέχει το κέντρον του Κόσμου. Το Βιβλίον II διδάσκει την διαίρεσιν τής ουρανίου σφαίρας εις ζώνας και τα φαινόμενα, διά των Οποίων επιση­μαίνεται ή ανατολή και ή δύσις των αστέρων. Η διάρκεια του έτους και η θεωρία του ηλίου δίδει ύλην εις το Βιβλίον III, η διάρκεια των μηνών και η θεωρία της σελήνης δίδει ύλην εις το Βιβλίον IV.

Το Βιβλίον V ασχολείται με την περιγραφήν και κατασκευήν του περίφημου, οργάνου, το οποίον εκαλείτο αστρολάβος, το σπουδαιότερον όργανον των αρχαίων αστεροσκοπείων, όπερ εχρησιμοποίησε και ο Δανός αστρονόμος Tycho Brahe (1546-1601) εις τας παρατηρήσεις του. Το Βιβλίον VI ασχολείται με τα φαινόμενα των «συζυγιών» και «αντιζυγιών» των μεγάλων άστρων Ηλίου και Σελήνης και με τας σχέσεις αυτών προς τα φαινόμενα των εκλείψεων.

Τα δύο επόμενα βιβλία είναι αφιερωμένα εις τους απλανείς αστέρας και την σπουδαιότατην και περιφανή ανακάλυψιν του Ίππαρχου, την γνωστήν υπό τον αστρονομικόν όρον «μετάπτωσις των Ισημεριών». Τα τελευταία πέντε βιβλία είναι αφιερωμένα έκαστον εις ένα των πλανητών Ερμήν Αφροδίτην, Άρην, Δία και Κρόνον.

Εις τους ανωτέρω υποδειχθέντας λόγους, ιστορικού χαράκτηρος, διά τούς οποίους η Αλμαγέστα παρουσιάζει τόσον πλούσιον ενδια­φέρον, πρέπει να προστεθή και ένας τρίτος, ακόμη σπουδαιότερος. Ότι το έργον αυτό αποτελεί την αρχαιοτέραν συγγραφικήν εργασίαν, εις την οποίαν περιέχονται πολυάριθμα στοιχεία και θαυμάσιοι εφαρμογαί της σφαιρικής τριγωνομετρίας, επιστήμης μη χωριζόμενης πλέον από το πλευρόν της Αστρονομίας, αν όχι προηγουμένως διά των εργασιών του Αρχιμήδους, τουλάχιστον από τής ημέρας, καθ' ην ο Ίππαρχος καθώρισεν επί της ουρανίου σφαίρας την θέσιν των άστρων διά τής χρήσεως σφαιρικών συντεταγμένων (πλάτους και μήκους). Επειδή όμως εκ της σφαιρικής τριγωνομετρίας ο Πτολεμαίος περιέλαβε μόνον όσα ήσαν αναγκαία εις τον σκοπόν του, δεν πρέπει να θεωρούμεν ότι αι προτάσεις, τας οποίας αναφέρει, εκπροσωπούν το σύνολον των γνώσεων των Ελλή­νων έπη του θέματος, μολονότι δεν έχομεν δυστυχώς δεδομένα επιτρέποντα την συμπλήρωσιν.

Η Πτολεμαϊκή Τριγωνομετρία φαίνεται, χωρίς αμφιβολίαν, πολύ διάφορος της ιδικής μας, διότι δεν απαντώνται εις εκείνην αι συνήθεις εις ημάς τριγωνομετρικοί συναρτήσεις, άλλα μόνον αι χορδαί των θεω­ρουμένων τόξων. Παρά ταύτα, αρκεί εις τα θεωρήματα της Αλμαγέστας να θέσωμεν όπου «χορδή χ» το ισοδύναμον «2ημχ/2», διά ν' αποκαταστήσωμεν την ουσιαστικήν ταυτότητα των δύο συστημάτων.

Η δημιουργία ενός υποκατάστατου της θεωρίας των κυκλικών συναρ­τήσεων υπήρξεν αποτέλεσμα της συχνής ανάγκης, πού παρουσιάζετο εις τους αστρονόμους, να έχουν ένα πίνακα τιμών των χορδών τόξων πολλα­πλασίων ενός τόξου  περιφερείας⁽²⁾. Τοιαύτη  ανάγκη, διαπιστωθείσα από τον Ίππαρχον (αν όχι προηγουμένως), ικανοποιήθη υπό τούτου εις ένα έργον εκ δώδεκα βιβλίων, δυστυχώς απολεσθέν. Προσθέτομεν ότι δεν αποκλείεται εις την εργασίαν αυτήν να είχε μερικούς προδρόμους, γενάρχης των οποίων θα ήτο, κατά τινά μαρτυρίαν, ο Απολλώνιος ο Περγαίος, ή ακόμη ίσως και ο Αρχιμήδης. Εφ' όσον όλα αυτά τα έργα εχάθησαν, μόνον η Αλμαγέστα δύναται να μας φωτίση ως προς τον τρόπον, με τον όποιον οι αρχαίοι επέτυχον του σκοπού των.

Μανθάνομεν από το μέγα αυτό έργον, ότι εντελώς αναλόγως προς ο,τι συνηθίζεται σήμερον, ήρχιζαν από τον υπολογισμόν των χορδών μερικών αξιοσημείωτων τόξων, εφαρμόζοντες το Πυθαγόρειον Θεώρημα και. τας σχέσεις ακτίνος κύκλου προς τας πλευράς των απλούστερων εγγεγραμμένων κανονικών πολυγώνων (σχέσεις γνωστάς από τα Στοιχεία του Ευκλείδου).

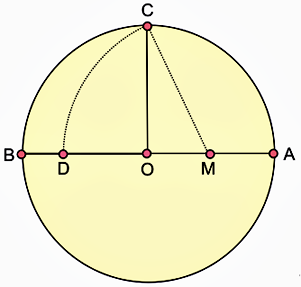
Αρμόζει ν' αναφέρωμεν μίαν κατασκευήν των πλευρών του εις κύκλον εγγεγραμμένου κανονικού πενταγώνου και δεκαγώνου εξαιρετικής απλότητος: Εις δεδομένον κύκλον (σχ. 1) άγεται η διάμετρος ΑΒ και η επ' αυτήν κάθετος ακτίς ΟC. Εάν είναι Μ το μέσον της ακτίνος ΟΑ, γράφομεν με κέντρον το σημείον τούτο και ακτίνα ΜC τόξον περιφερείας τέμνον εις D την ακτίνα ΟΒ. Θα είναι τότε CD η πλευρά του κανονικού πενταγώνου και ΟD η πλευρά του κανονικού δεκαγώνου, πού εγγράφονται εις τον δοθέντα κύκλον.

Σχήμα 1

Η εν λόγω κατασκευή αναγράφεται επίσης ανωνύμως εις τον Αντλαντικόν Κώδικα (Codice Atlsntico) του Leonardo da Vinci, είναι δε ανάλογος, αλλά απλουστέρα μίας άλλης προταθείσης εις τον Gauss δι' επιστολής υπό χρονολογίαν 17 Φεβρουαρίου 1814 (Αλληλογραφία μεταξύ C. F. Gauss και C. L. Gerling, Βερολίνον 1927), την οποίαν κατασκευήν ας μας επιτραπή ν' αναφέρωμεν: Με τα αυτά δεδομένα (σχ. 2), ας άχθη εις το σημείον Α η εφαπτομένη της περιφερείας και ας ληφθή επ' αυτής το τμήμα ΑΒ ίσον προς το ήμισυ της ακτίνος.

Σχήμα 2

Άγεται η ευθεία ΟΒ και λαμβάνομεν επ' αυτής ΒC = ΒΑ. Αν η ευθεία ΑC προεκτεινομένη τέμνη την περιφέρειαν εις D, θα είναι η ΟD κάθετος επί την ΟΒ, η ΟC πλευρά του κανονικού δεκαγώνου και η CD πλευρά του κανονικού πενταγώνου, εγγεγραμένων εις τον δοθέντα κύκλον.

Επειδή η χρήσις των κανονικών πολυγώνων περιορίζει μοιραίως την προσπάθειαν εις ειδικάς κατηγορίας  τόξων,  ο Πτολεμαίος ησθάνθη την ανάγκην να καταφυγή εις θεώρημα γενικού χαρακτήρος και ούτω διετύπωσε την ακόλουθον πρότασιν: «Εάν ΑΒCD είναι τετράπλευρον εγγεγραμμένον εις περιφέρειαν, το άθροισμα των γινομένων των ζευγών αντικειμένων πλευρών αυτού, ΑΒ • CD .και ΑD • ΒC, είναι ίσον προς το γινόμενον των διαγωνίων ΑC • ΒC». Αυτό είναι το σημαντικόν θεώρημα που φέρει ακριβώς σήμερον το όνομα του Πτολεμαίου, όχι τόσον διά να επιβεβαιώνη την υπ' αυτού ανακάλυψίν του, όσον δια να υπενθυμίζη ότι το θεώρημα απαντάται διά πρώτην φοράν εις το αθάνατον έργον του. Εφαρμόζων τούτο ο Πτολεμαίος μετά τίνων προφυλάξεων, έφθασεν εις θεμελιώδη εξαγόμενα, τα όποια σήμερον εκφράζονται με τους γνωστούς τύπους τής Τριγωνομετρίας :

ημ (x - y) = ημ x • συν y - συν x • ημ y

συν(x + y) = συν x • συν y - ημ x • ημ y

Εκ τούτων, όπως είναι γνωστόν, εξάγονται όλαι αι άλλαι σχέσεις αι αποτελούσαι την σημερινήν θεωρίαν των κυκλικών συναρτήσεων. Ούτω ο Πτολεμαίος εξάγει π.χ. την σχέσιν:

την οποίαν κατόπιν εφαρμόζει κατ' επανάληψιν διά να υπολογίση την σει­ράν των χορδών την αρχομένην από του τόξου 12°, ούτινος η χορδή είχεν ήδη προηγουμένως υπολογισθή, και φθάνουσαν εις το τόξον 3/4 μοίρας. Το τελευταίον θεωρητικόν στοιχείον, πού ήτο αναγκαίον εις τον Πτολεμαίον διά την κατασκευήν του ζητουμένου πίνακος χορδών, συνί­στατο εις ένα θεώρημα, απαντώμενον ήδη εις τον Αρίσταρχον και τον Αρχιμήδη και διατυπούμενον ως έξης : «Εάν x, y είναι δύο τόξα μικρό­τερα του τετάρτου περιφερείας και είναι x > y, θ' αληθεύη δι αυτά η σχέσις:

Με την βοήθειαν του θεωρήματος τούτου ο Πτολεμαίος φθάνει εις εκτίμησιν της χορδής 1°, δυνάμεθα δε να εκτιμήσωμεν την ακρίβειαν του ευρεθέντος αποτελέσματος παρατηρούντες ότι, εάν ταυτισθή η χορδή μετά του αντιστοίχου τόξου, προκύπτει ως μήκος περιφερείας, διαμέτρου ίσης. προς την μονάδα, η τιμή:

η οποία έχει ακριβή τρία δεκαδικά ψηφία.

Εκμεταλλευόμενος τα διάφορα αυτά αποτελέσματα ο Πτολεμαίος υπο­λογίζει τας χορδάς όλων των τόξων, πού είναι πολλαπλάσια του τόξου 1/2 μοίρας και δεν υπερβαίνουν τας 180°, υπό την προϋπόθεσιν ότι η διά­μετρος του κύκλου εκφράζεται διά του αριθμού 120. Κατ' ουσίαν πρόκει­ται περί καταστρώσεως ενός πίνακος ημίτονων όλων των τόξων, πού είναι πολλαπλάσια του τόξου 1/4 μοίρας και δεν υπερβαίνουν τας 90°, του οποίου η ακρίβεια δύναται να εκτιμηθή εκ της παρατηρήσεως ότι διά το ημ30' δίδει μίαν τιμήν με ακριβή τέσσαρα δεκαδικά ψηφία. Επειδή δεν διαφεύγει του Πτολεμαίου το γεγονός, ότι δια τής εφαρμοζόμενης μεθόδου τα σφάλματα προστίθενται τα μεν εις τα δε, ελέγχει και διορθώ­νει τα εξαγόμενα διά συγκρίσεως των τιμών, τας οποίας υπελόγισε προη­γουμένως κατ' ευθείαν διά μίαν σειράν αξιοσημείωτων τόξων.

Ο έχων προ οφθαλμών το γενικόν διάγραμμα της ύλης των σημερι­νών βιβλίων τριγωνομετρίας, θα κάμη ασφαλώς την υπόθεσιν, ότι ο Πτο­λεμαίος, μετά την αποκατάστασιν μιας θεωρίας ισοδυνάμου προς την ιδικήν μας θεωρίαν των κυκλικών συναρτήσεων, εστράφη προς την επίλυσιν των ευθυγράμμων τριγώνων, όπου ευρίσκει άμεσον έφαρμογήν. Τίποτε όμως παρόμοιον δεν απαντάται. Αν και απέδειξε με ένα παράδειγμα ότι ήτο εις θέσιν να υπολογίση όλα τα στοιχεία ενός σχήματος, όταν εδίδετο επαρκής αριθμός πλευρών και γωνιών, εντούτοις δεν προβαίνει εις μεθοδικήν ανάπτυξιν ενός συστήματος λογισμού. Και επειδή ακριβώς, προκει­μένου περί σφαιρικών τριγώνων, ακολουθεί διαμετρικώς αντίθετον τακτικήν, θεμελιούται εις την ιστορίαν των μαθηματικών το, περιεργότατον γε­γονός ότι η σφαιρική τριγωνομετρία προηγήθη ιστορι­κώς  της  επιπέδου.

Ως θεωρητικόν θεμέλιον τής σφαιρικής τριγωνομετρίας εκλέγει ο Πτολεμαίος το θεώρημα του Μενελάου διά τα σφαιρικά τρίγωνα. Προστρέχει εις αυτό οσάκις έχει ανάγκην να έκφραση κάποιο στοιχείον σφαιρικού τριγώνου μέσω επαρκών δεδομένων άλλων στοιχείων του. Διά το ορθογώνιον εις Α σφαιρικόν τρίγωνον ΑΒC με πλευράς τα τόξα a,b,c ευρίσκει π.χ. τας γνωστάς σχέσεις :

ημc = ημa · ημC

εφc = ημb · εφC

εφc = εφa · συνΒ

Και επειδή αι ανωτέρω σχέσεις δεν είναι αι μόναι εφαρμογαί, τας οποίας δύναται να δώση το θεώρημα του Μενελάου, καταδεικνύεται ότι τούτο δύναται να καταλάβη εις την σφαιρικήν τριγωνομετρίαν θέσιν πολύ σπουδαιοτέραν εκείνης, την οποίαν του δίδουν εις τα σύγχρονα εγχειρίδια.

Όπως συμβαίνει εις όλα τα έργα τα θεωρούμενα κλασικά, ούτω και προκειμένου περί της Αλμαγέστας, δεν έλλειψαν οι σχολιασταί. Ο γνωστότερος εξ αυτών είναι ο Θέων ο Αλεξανδρεύς, ζήσας μεταξύ IV και V αιώνος μ.Χ. υπό την βασιλείαν Θεοδοσίου του Μεγάλου, και γνωστός, εις την ιστορίαν δια μίαν επιμελημένην έκδοσιν των Στοιχείων του Ευκλείδου. Το αστρονομικόν του έργον, τουλάχιστον εν μέρει (ίσως όμως και εξ ολοκλήρου, διότι δεν είναι βέβαιον ότι επεξέτεινε τας διασαφήσεις, του εις ολόκληρον την Αλμαγέσταν) αντέστη νικηφόρος εις την καταστρεπτικήν μανίαν του χρόνου, με περιωρισμένον όφελος διά την επιστήμην και την ιστορίαν, διότι πολύ μικράν βοήθειαν προσφέρει εις. τους μελετητάς του μεγάλου έργου του Πτολεμαίου, καθώς και εις τους επιθυμούντος ν' αντλήσουν πληροφορίας περί τής εξελίξεως τής ελληνικής, αστρονομίας μέχρι των ημερών αυτού. Δεν συντρέχει λοιπόν κανείς λόγος, να ενδιατρίψωμεν αναλύοντες το πτωχόν αυτό κείμενον του μετρίου αλεξανδρινού υπομνηματιστού⁽³⁾. Αντιθέτως είναι καθήκον μας να μνημονεύσωμεν δύο άλλα αξιόλογα έργα του συγγραφέως της Μαθηματικής Συναγωγής, τα όποια έφθασαν μέχρις ημών.

Το ένα φέρει τον τίτλον Ανάλημμα και έχει ως θέμα την ορθήν προβολήν μιας σφαίρας εφ' ενός επιπέδου, εις υποβοήθησιν της χαράξεως των ηλιακών ωρολογίων (μεσημβρινών). Το άλλο, πού φέρει τον τίτλον Άπλωσις επιφανείας έχει ως αντικείμενον την κεντρικήν προβολήν τής επιφανείας μιας σφαίρας επί του ισημερινού επιπέδου από του βορείου πόλου. Πρόκειται λοιπόν περί της μεθόδου απεικονίσεως εφ' ενός επιπέδου μιας σφαίρας, μεθόδου γνωστής σήμερον υπό το όνομα στερεογραφική προβολή. Ο Πτολεμαίος εγνώριζε μίαν των θεμελιωδών ιδιοτήτων, καθ' ην γίνεται η αντιστοιχία μιας περιφερείας της σφαίρας, προς μίαν περιφέρειαν του επιπέδου, και προέβη εις χρησίμους εφαρμογάς.

Τελειώνομεν με την παρατήρησιν ότι εις το περισσότερον διαδεδομένον έργον του, δηλαδή την Γεωγραφικήν αφήγησιν, εις 8 βιβλία, ο Πτολεμαίος χρησιμοποιεί άλλην μέθοδον απεικονίσεως σφαίρας επί επιπέδου, η οποία ενέπνευσεν εις τον Μερκάτορα την εφαρμογήν αυτής εις τους χάρτας των ναυτιλλομένων, πού φέρουν σήμερον το όνομα Μερκατορικοί χάρται.

Το συμπέρασμα είναι ότι εις την αρχαίαν έλληνικήν βιβλιογραφίαν υφίστανται αι θεωρητικαί βάσεις των τριών κυριωτέρων μεθόδων, αι οποίαι εφηρμόσθησαν ως επί το πλείστον, διά την επί επιπέδου απεικόνισιν της γηίνης επιφανείας.

__________________________________________________________

1. Το μόνον διασωθέν έργον του Ίππαρχου (120 π.Χ.) είναι ένα μικράς σημασίας σχόλιον εις ποίημα του Αράτου και εις Εύδοξον, υπάρχει δε του σχολίου τούτου μία πρόσφατος έκδοσις.
2. Ήτο μία ανάγκη, η όποια από γεωμετρικής απόψεως είχε γίνει αισθητή εις τον Αρχιμήδη, ως προκύπτει από ένα έργον, εκ του οποίου εσώθη μικρόν απόσταμα.
3. Από το έργον του Θέωνος Σχόλιον εις την Αλμαγέσταν ήσαν γνωστά τα αφορώντα τα βιβλία Ι και II, εθεωρείτο δε απολεσθέν το κείμενον το αφορών το βιβλίον III. Ανευρέθη όμως και τούτο υπό του Α. Rome εις την εθνηκτήν βιβλιοθήκην της Φλωρεντίας. Πληροφορίαι σχετικοί προς την ανακάλυψιν αυτήν ευρίσκονται εις άρθρον του ιδίου Le troisieme livre des commentaires sur l' Almageste, par Theon et Hypathie (Publications du laboratoire d' Astronomie et de Geodesie de l' Universite de Louvain, vol. III, 1916).. Συνάγεται εξ, αυτού ότι εις το έργον του ο Θέων εβοηθήθη από την κόρην του Υπατίαν, την πολυμαθή συγγραφέα, η οποία, ως είδομεν (§ 62), κατεκρεουργήθη βαναύσως εις τας οδούς τής Αλεξανδρείας το 415 κατά την διάρκειαν των συγκρούσεων μεταξύ της καταρρεούσης ειδωλολατρίας και του οικουμενικώς διαδιδομένου χριστιανισμού. Εις την Ιστορίαν μας η Υπατία, ανεξαρτήτως του μαρτυρικού της θανάτου, είναι αξία μνείας,., διότι είναι η πρώτη εις την σειράν των γυναικών, αι οποίαι κατέλιπον ίχνη ως εργάτιδες των ακριβών επιστήμων.