Αρχιμήδης ο Συρακούσιος

G.LORIA

ΙΣΤΟΡΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ

Ο Αρχιμήδης, εγεννήθη το 287 π.Χ. εις Συρακούσας. Κατά τινάς, πατήρ του ήτο ο αστρονόμος Φειδίας, γνωστός από μίαν προσπάθειάν του να προσδιορίση την σχέσιν των μεγεθών μεταξύ Ηλίου και Σελήνης. Όλοι περαιτέρω συμφωνούν με την γνώμην ότι ο Αρχιμήδης συνεδέετο διά δεσμών συγγενείας και φιλίας με τον τότε βασιλικόν οίκον της γενεθλίου του πόλεως.

Υπήρξε περίλαμπρον παράδειγμα πρωτοτύπου ερευνητού, ο οποίος, μη ενδιαφερόμενος ποσώς να ομαλύνη τον δρόμον εις τους αρχαρίους, απορ­ροφάται αποκλειστικώς και μόνον εις την αποκάλυψιν νέων αληθειών προς ικανοποίησιν εαυτού και των ωρίμων ήδη διανοουμένων. Αυτός είναι και ο λόγος, διά τον όποιον, ενώ η κατανόησις του Ευκλείδου δεν απαιτεί εξαιρετικήν προπαιδείαν και ευφυΐαν, τα προϊόντα της μαθηματικής σκέψεως, τα όποια πρόκειται τώρα να έξετάσωμεν, είναι προσιτά αποκλειστικώς και μόνον εις αναγνώστας υψηλής πνευματικής στάθμης.

Μετέβη δι' εκπαιδευτικούς σκοπούς εις Αίγυπτον, ελθών εις επαφήν, όχι βέβαια με τον Ευκλείδη, πού είχεν εν τω μεταξύ αποθάνει, αλλά με τους διαδόχους του, συνάψας δεσμούς στενής φιλίας με εξέχοντας γεωμέτρας (όπως ο Κόνων ο Σάμιος, ο Ερατοσθένης ο Κυρηναίος, ο Δοσίθεος κλπ), εις τους οποίους κατόπιν αφιέρωσεν όσα έργα συνέταξε, μετά την επιστροφήν του εις την πατρίδα.

Εκεί αφιέρωσεν εαυτόν εξ ολοκλήρου εις γεωμετρικός και μηχανικάς μελετάς. Όταν όμως, διαρκούντος του β' καρχηδονιακού πολέμου, η πόλις των Συρακουσών, ως σύμμαχος της Καρχηδόνος, περιεκυκλώθη από τον ρωμαϊκόν στρατόν, ο Αρχιμήδης έθεσε την ιδιοφυΐαν του εις την υπηρεσίαν της πατρώας γης και απεδείχθη τόσον καταπληκτικά γόνιμος εις την επινόησιν πρωτοτύπων όπλων, αμυντικών και επιθετικών (αρκεί να μνημονεύσωμεν τους φοβερούς καταπέλτας και τα θρυλικά καυστικά κάτοπτρα), ώστε παρουσίασε το μοναδικόν εις την ιστορίαν φαινόμενον ενός ανδρός μαχόμενου μόνου επί μίαν τριετίαν εναντίον ολοκλήρου στρα­τεύματος. Μόνον όταν η πολιορκία μετετράπη εις στενόν αποκλεισμόν και τα όπλα της προδοσίας εβοήθησαν τον πολιορκητήν, ο ύπατος Κλαύ­διος Μάρκελλος ηδυνήθη να καταβάλη τον μαθηματικόν εκείνον Βριά­ρεω, με τον όποιον ευρίσκετο εις πόλεμον. 

Κατά την διάρκειαν της λεηλασίας, η οποία ηκολούθησε την κατάληψιν των Συρακουσών (212 π.Χ.), ο Αρχιμήδης εφονεύθη υπό ρωμαίου στρατιώτου, παρά τας ρητάς διαταγάς τας δοθείσας υπό του Μαρκέλλου, όπως φεισθούν της ζωής του.

Εις μνήμην του ηγέρθη αντάξιος τάφος, επί του οποίου, κατ' εκφρασθείσαν άλλοτε επιθυμίαν του εχαράχθη σφαίρα εγγεγραμένη εις κύλινδρον, διά να υπενθυμίζη εις τους επερχόμενους ένα από τα ωραιότερα ευρήματα της οξυνοίας του. Από το σχήμα τούτο ανεκαλύφθη βραδύτερον το μνημείον, αναγνωρισθέν από τον Κικέρωνα, όταν κατά το 75 π.Χ. υπηρέτησεν ως ταμίας, εις Σικελίαν. Σήμερον δεν υπάρχει πλέον κανένα ίχνος του μνημείου.

Προκειμένου να εξετάσωμεν τα σωζόμενα έργα του Αρχιμήδους, δεν είναι δυνατόν ν' ανατρέξωμεν εις την χρονολογικήν σειράν, μόνην ικανήν να παράσχη αυθεντικήν εικόνα της εξελικτικής πορείας των ιδεών οιουδήποτε στοχαστού, καθ' όσον ελλείπουν τ' απαιτούμενα δεδομένα. Θα τηρήσωμεν λοιπόν, κατ' ανάγκην, άλλην σειράν, εναρμονιζομένην προς τα αντικείμενα των εργασιών.

Και είναι λογικόν ν' αρχίσωμεν την ανάλυσίν μας από την σπουδαιοτάτην συμβολήν του Συρακούσιου μαθηματικού εις τα προβλήματα του τετραγωνισμού του κύκλου και της ευθειοποιήσεως της περιφερείας, των οποίων την ουσιαστικήν ταυτότητα πρώτος έφερεν εις φως, διά του γνωστού θεωρήματος του : «πᾶς κύκλος ἴσος ἐστὶ τριγώνῳ ὀρθογωνίῳ, οὐ μὲν ἐκ τοῦ κέντρου ἴση μιᾷ τῶν περὶ τὴν ὀρθήν, ἡ   δὲ   περίμετρος τῇ βάσει».

Κατ' αντίθεσιν προς τους προγενεστέρους γεωμέτρας ο Αρχιμήδης, δεν επέμεινεν επί της προσπάθειας να λύση διά του κανόνος και του διαβήτου ένα πρόβλημα, το όποιον απαιτεί εντελώς άλλα μέσα, αλλ' αντικαθιστών την ιδέαν της κατασκευής με την απαίτησιν της μ ε τ ρ ή σ ε ω ς, ετέθη επί της μόνης οδού, η οποία, κατά την εποχήν του, ηδύνατο να δώση ικανοποιητικόν αποτέλεσμα, τουτέστι να προσδιορίση με επαρκή προσέγγισιν τον λόγον π της περιφερείας προς την διάμετρον. Προς τον σκοπόν τούτον κατέφυγεν εις την θεώρησιν κανονικών πολυγώνων, εγγεγραμμένων και περιγεγραμμένων, όπως είχον ήδη κάμει, με ανάλογους προθέσεις, ερευνηταί της προγενεστέρας περιόδου, οι Αντιφών και Βρυσών. Εκκινών από το κανονικόν εξάγωνον και αναδιπλασιάζων διαδοχικώς τον αριθμόν των πλευρών, έφθασε, διά του κανονικού πολυγώνου  96 πλευρών, εις την περιώνυμον προσέγγισιν :

εις την οποίαν εσταμάτησε, θεωρών το αποτέλεσμα τούτο ως επαρκώς ακριβές τόσον μάλλον, καθ' όσον οι επιθυμούντες μεγαλυτέραν ακρίβειαν δεν είχον παρά να προχωρήσουν ακόμη περισσότερον εις την οδόν, που ήνοιξεν ο Αρχιμήδης.

Θα ίδωμεν κατόπιν, ότι τοιαύτη σιωπηρά πρόκλησις εγένετο δεκτή από πολλούς, προς το παρόν όμως παρατηρούμεν, ότι ο Αρχιμήδης εφαρμόζων την πρότασιν, πού εμνημονεύσαμεν ανωτέρω, κατέληξεν εις το συμπέρασμα ότι «ὁ κύκλος πρὸς τὸ ἀπὸ τῆς διαμέτρου τετράγωνον, λόγον ἔχει, ὅν 11 πρὸς   14»,   συμπέρασμα παρέχον  το εμβαδόν του κύκλου, με μεγάλην προσέγγισιν, ίσον προς 11/14 του τετραγώνου της διαμέτρου

Τα συμπεράσματα αυτά αποτελούν τα πρώτα συγκεκριμένα και χρήσιμα δεδομένα, τα όποια απέδωσαν αι καταβληθείσαι προσπάθειαι προς λύσιν του διασημότερου προβλήματος, εξ όσων συναντώνται εις ολόκληρον την γεωμετρίαν.

Τα συμπεράσματα αυτά αποτελούν τα πρώτα συγκεκριμένα και χρήσιμα δεδομένα, τα όποια απέδωσαν αι καταβληθείσαι προσπάθειαι προς λύσιν του διασημότερου προβλήματος, εξ όσων συναντώνται εις ολόκληρον την γεωμετρίαν.

Το τεύχος το τιτλοφορούμενον κύκλου μέτρησις αποτελεί εράνισμα, προς σχολικήν χρήσιν, από μίαν εκτενεστέραν εργασίαν επί του αντικειμένου τούτου, το πρωτότυπον της οποίας δεν ανευρέθη μέχρι σημερον. Κατά τινάς, εις την εργασίαν ταύτην ο Αρχιμήδης είχε προωθήσει την προσέγγισιν μέχρι της τιμής π = 3,1416, ανταποκρινόμενης εις κανονικόν πολύγωνον   

  πλευρών.

Την  προσέγγισιν δε ταύτην εκαυχήθησαν ότι επέτυχον και οι Ινδοί, χωρίς όμως να παρουσιάσουν τεκμήρια εις υποστήριξιν του ισχυρισμού των. Υπάρχει όμως ένα ντοκουμέντον πολύτιμον, εν σχέσει προς το περιεχόμενον του έργου του Αρχιμήδους, μαρτυρούμενον από ένα πολυμαθέστατον Άραβα, τον, τον Al-Biruni. Ούτος αποσπά από την εν λόγω εργασίαν του Aρχιμήδους την ακόλουθον πρότασιν : «εις ένα κύκλον εγγράφεται η τεθλασμένη ACD. Έστω Β το μέσον του τόξου ACD, και αχθήτω η ΒΗ κάθετος επί την ΑC. Θα ισχύη τότε η σχέσις:

 ΑΗ = ΗC + CD».

Σχήμα 1

από την ανωτέρω εκφώνησιν η πρότασις έχει έξαφανισθή από την μαθηματικήν βιβλιογραφίαν, Εάν όμως εισαγάγωμεν τας γωνίας

 ,

η ανωτέρω πρότασις αποδεικνύεται ευκόλως ότι είναι ισοδύναμος προς την ακόλουθον σχέσιν :

ημ (α — β) = ημα συνβ  - συνα ημβ.

Εξ άλλου εκ της προφανούς ισότητος :

ΑC = ΑΗ + ΗC,

προκύπτει η  συζυγής σχέσις :

ημ (α + β) = ημα συνβ + συνα ημβ,

και επειδή εξ αυτών των σχέσεων έπονται αι ανάλογοι εκφράσεις δια το συν (α ± β), φθάνομεν εις το απροσδόκητον συμπέρασμα, ότι εις τον μέγαν Συρακούσιον δεν ήσαν άγνωστοι αι προτάσεις αι ισοδυναμούσαι προς τους συνήθεις τριγωνομετρικούς τύπους διά την πρόσθεσιν και αφαίρεσιν των τόξων.

Είναι ευνόητον, ότι αι εργασίαι αύται του Αρχιμήδους επί της απλουστέρας των καμπύλων γραμμών, πού έγιναν αντικείμενον ερεύνης εκ μέρους των αρχαίων, ημπορούν να θεωρηθούν ως συμπληρώματα εις τα Στοιχεία του Ευκλείδου.

Ανάλογον χαρακτήρα έχουν δύο άλλα βιβλία περί σφαίρας και κυλίνδρου, αφού η ύλη πού εκτίθεται εις αυτά έγινεν ήδη αναπόσπαστον μέρος όλων των εγχειριδίων της στοιχειώδους γεωμετρίας. Εις το Βιβλίον Ι πράγματι διδάσκονται κομψαί εκφράσεις διά την παράπλευρον επιφάνειαν και τον όγκον ενός κυλίνδρου ή ενός κολούρου κώνου προκύπτοντος διά τομής του ορθού κώνου με επίπεδον παράλληλον προς την βάσιν, διά την επιφάνειαν και τον όγκον σφαίρας η σφαιρικού τομέως. Ο Αρχιμήδης συνδυάζων ευφυέστατα τοιαύτας εκφράσεις, έφθασεν εις σπουδαίας σχέσεις μεταξύ των ανωτέρω μεγεθών.

Των σχέσεων τούτων υποδεικνύει εφαρμογάς εις το βιβλίον II και συγκεκριμένως εις την λύσιν πολλών προβλημάτων σκοπούντων εις την κατασκευήν σφαίρας ισοδυνάμου προς κώνον ή κύλιδρον, την διαίρεσιν σφαίρας δι' επιπέδου εις τμήματα, των όποιων αι έπιφάνειαι και οι όγκοι έχουν μεταξύ των δοθέντα λόγον. Μερικά ισοδυναμούν προς την λύσιν εξισώσεων πρώτου και δευτέρου βαθμού, άλλα ανάγονται εις τον διπλασιασμόν του κύβου και άλλα εις την λύσιν της πλήρους τριτοβαθμίου εξισώσεως. Ο Αρχιμήδης θεωρεί άσκοπον να εισέλθη εις τας λεπτομέρειας της λύσεως, πού θα ήσαν τόσον επιθυμητοί, παραπέμπων τον αναγνώστην εις το τέλος της πραγματείας του. το όποιον όμως δυστυχώς δεν περιεσώθη. Οι σχολιασταί του δεν μας παρέχουν επ' αυτού παρά εξηγήσεις ελλιπείς και αποσπασματικάς, διό και αι αρχαίαι μέθοδοι λύσεως των εξισώσεων 3ου βαθμού αποτελούν ένα από τα πλέον βασανιστικά αινίγματα, πού απαντώνται εις την ιστορίαν της ελληνικής γεωμετρίας. Εις την διαλεύκανσιν του αινίγματος τούτου κατέβαλον τεραστίας προσπάθειας οι βαθύτεροι γνώσται της αρχαίας γεωμετρίας, χωρίς να επιτύχουν οριστικήν λύσιν αυτού.

Τα θεωρήματα, περί των οποίον εγένετο λόγος, ημπορούν, τουλάχιστον εν μέρει, να θεωρηθούν ως μερικαί περιπτώσεις άλλων, αναφερομένων εις τας επιφανείας πού γεννώνται εκ περιστροφής μιας ελλείψεως περί ένα των αξόνων της, μιας παραβολής περί τον άξονα της, η ενός κλάδου υπερβολής περί τον άξονα της συμμετρίας του. Τα αξιολογώτατα αυτά σχήματα εξετάξει ο Αρχιμήδης εις ένα άλλο θαυμάσιον βιβλίον του τιτλοφορούμενον περί κωνοειδέων και σφαιροειδέων. Εξ αυτού μανθάνομεν τας σχέσεις των όγκων των σχημάτων, πού γεννώνται διά τομής μιας των ανωτέρω επιφανειών υπό επιπέδων καθέτων επί τον άξονα. Λαμβάνονται δε αι σχέσεις αύται δι' ευφυέστατων συλλογισμών, οι όποιοι αποτελούν αληθείς και καθαράς ολοκληρώσεις υπό άλλο ένδυμα και αι οποίαι εχρησίμευσαν ως κίνητρα, και ως οδηγοί διά τας άλλας ομοίου τύπου έρευνας, πού έγιναν εις την γεωμετρίαν προ της δημιουργίας του ολοκληρωτικού λογισμού.

Προτού επιχειρήση τους λεπτούς αυτούς υπολογισμούς, ο Αρχιμήδης εχρειάσθη να επιμείνη εις την έκθεσιν μερικών ουσιωδών ιδιοτήτων των επιφανειών, των οποίων προηγουμένους εδόθη ο ορισμός (πρόκειται περί όλων των διά περιστροφής κωνικών τομών παραγομένων επιφανειών, έκτος του μονοχώνου υπερβολοειδούς), επέτυχε δε τούτο μέσω σειράς σκέψεων μεγάλης αξίας, πού κατέστη μεγαλύτερα αφ' ότου κατεδείχθη η δυνατότης της εφαρμογής των εις οιανδήποτε επιφάνειαν δευτέρου βαθμού. Είτε είναι, είτε δεν είναι ο Αρχιμήδης ο πρώτος ασχοληθείς με τας επιφανείας αυτάς, είναι εκτός πάσης αμφιβολίας, ότι εις αυτόν οφείλεται το ότι αύται εγένοντο αντικείμενον ιδιαιτέρας προσοχής και φροντίδος εκ μέρους των μαθηματικών.

Ανάλογον δόξαν απέκτησεν ο μέγας γεωμέτρης των Συρακουσών με μίαν άλλην εργασίαν του περί ελίκων. Εις την εργασίαν αυτήν γίνεται μεθοδική σπουδή των καμπύλων (αι οποίαι φαίνεται απησχόλησαν διά πρώτην φοράν τον Κόνωνα τον Σάμιον), των παριστωμένων εις πολικάς συντεταγμένος δι' εξισώσεων τής μορφής ρ = αω, ένθα α μία σταθερά ^[1]. Αι καμπύλαι αύται ονομάζονται κοινώς σήμερον έλικες του Αρχιμήδους προς διατήρησιν τής μνήμης εκείνου, όστις. πρώτος ανεκάλυψε και απέδειξε τας θεμελιώδεις των ιδιότητας. Ο Αρχιμήδης πράγματι απεκάλυψε την δυνατότητα χρήσεως τοιούτων καμπύλων εις την ευθειοποίησιν όχι μόνον ολοκλήρου περιφερείας, άλλα και ενός τυχόντος τόξου της, υπέδειξε την χάραξιν της εφαπτομένης χρησιμοποιών, όπως λέγομεν σήμερον, την πολικήν υφαπτομένην και έδωσε πλήθος θεωρημάτων τετραγωνισμού, χαρακτηριζομένων υπό αφθάστου κομψότητος. Εάν δεν έκαμε λόγον περί ευθειοποιήσεως τόξου έλικος, τούτο εξηγείται εκ του γεγονότος ότι αύτη είναι ανέφικτος, χωρίς την χρήσιν της λογαριθμικής συναρτήσεως. Ο δρόμος τον οποίον ηκολούθησεν ο Συρακούσιος μαθηματικός διά την απόδειξιν των αποτελεσμάτων τούτων φαίνεται σήμερον μακρός και δύσβατος, διό και το έργον του περί ελίκων ευρίσκει σήμερον ολίγους αναγνώστας. Αλλά τα ευρεθέντα συμπεράσματα κατέλαβον μόνιμον θέσιν εις την μαθηματικήν επιστήμην και τούτο αποτελεί χωρίς αμφιβολίαν την ωραιοτέραν επιβράβευσιν δι' οιονδήποτε ερευνητήν.

Μεταξύ των άλλων εργασιών του Αρχιμήδους, αι οποίαι υπολείπονται προς εξέτασιν, μεγάλην σπουδαιότητα έχουν, όπως θα ίδωμεν, τα δύο βιβλία του περί επιπέδων ισορροπιών, εις τα όποια παρεμβάλλεται και μία άλλη εργασία του τιτλοφορουμένη συνήθως τετράγωνισμός της παραβολής, μολονότι ο Αρχιμήδης  ομιλεί πάντοτε περί ορθογωνίου κώνου τομάς. Τα βιβλία αυτά αποτελούν την πρώτην επιστημονικήν πραγματείαν της στατικής και έχουν γραφή με μίαν μέθοδον τόσον πολύ αυστηρώς σύμφωνον προς εκείνην του Ευκλείδου, ώστε μένει κανείς με την εντύπωσιν ότι έχει προ οφθαλμών ένα κεφάλαιον μιας γεωμετρίας τεσσάρων διαστάσεων, όπου κάθε σημείον χαρακτηρίζεται από τας ιδίας του συντεταγμένος και το ίδιόν του βάρος.

Το πρώτον εκ των αναφερθέντων βιβλίων αρχίζει με τον προσδιορισμόν των συνθηκών ισορροπίας μιας βαρείας ευθείας (ως εκπροσωπούσης μίαν ράβδον στερεάν) στηριζομένης εις κατακόρυφον υπομόχλιον. Εδώ τίθεται η αρχή του μοχλού, η οποία ώθησε τον Αρχιμήδη εις την υπέροχον και ουχί αβάσιμον δήλωσίν του «δός μοι πᾷ στῶ καὶ τᾶν γᾶν κινήσω». Προχωρεί κατόπιν εις την έρευναν των κέντρων βάρους των απλούστερων γεωμετρικών σχημάτων (παραλληλογράμμου, τριγώνου, τραπεζίου). Και επειδή είναι φυσική η περιέργεια να ζητήση κανείς να μάθη κατά ποιον τρόπον οι αρχαίοι συνέλαβον αυτάς τας εννοίας, είναι σκόπιμον να σημειώσωμεν σχετικώς ότι τίποτε το συγκεκριμένον δεν είναι γνωστόν, καθ' όσον οι ορισμοί των εν λόγο) εννοιών περιείχοντο εις προγενέστερον έργον του Αρχιμήδους (περί ζυγών), το όποιον θεωρείται σήμερον ως απολεσθέν, εκτός του τίτλου του. Τα προκύπτοντα αποτελέσματα εφαρμόζει εις την παραβολήν, καταλήγων εις το περιώνυμον θεώρημα: «πᾶν τμάμα περιεχόμενον ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομὰς ἐπιτρίτον ἐστὶ τοῦ τριγώνου τοῦ ἔχοντος βάσιν τᾶν αὐτὰν τῷ τμάματι καὶ ὕψος ἴσον» (παν παραβολικόν τμήμα είναι τα 4/3 του τριγώνου του έχοντος βάσιν την του παραβολικού τμήματος και ύψος το αυτό). Το θεμελιώδες αυτό θεώρημα ανήκει εις τον Αρχιμήδη, ο όποιος ούτω κατώρθωσε να τετραγωνίση διά πρώτην φοράν καμπυλόγραμμον χωρίον, μη περιοριζόμενον μόνον υπό ευθειών η περιφερειών. Επειδή όμως η μέθοδος διά της οποίας έφθασεν εις το συμπέρασμα τούτο περιέχει στοιχεία ανήκοντα εις την Μηχανικήν, ο μέγας γεωμέτρης εθεώρησεν υποχρέωσιν ν' αναπαραγάγη το θεώρημα διά μεθόδου καθαρώς γεωμετρικής. Η μέθοδος αύτη εκτίθεται εις την εργασίαν, πού φέρει τον τίτλον τετραγωνισμός παραβολής. Κατ' αυτήν το εμβαδόν του παραβολικού τμήματος προσδιορίζεται ως όριον του αθροίσματος των όρων φθινούσης γεωμετρικής προόδου με λόγον 1/4. Το αυτό σχήμα, δηλαδή το παραβολικόν τμήμα μελέτα κατόπιν εκ νέου ο Αρχιμήδης εις το Βιβλίον II με κύριον σκοπόν ν' αποδείξη ένα άλλο σπουδαίον θεώρημα, ότι δηλαδή «το κέντρον βάρους του παραβολικοΰ τμήματος ευρίσκεται επί της ευθείας πού συνδέει την κορυφήν και το μέσον της βάσεως αυτού και χωρίζει αυτήν εις τον λόγον 3/2».

Αποκαθιστά κατόπιν μίαν βοηθητικήν πρότασιν (λήμμα), η οποία επιτρέπει τον προσδιορισμόν του κέντρου βάρους ενός σχήματος προκύπτοντος από άλλο δι' αποκοπής ωρισμένου τμήματος του. Ούτω κατορθώνει να γενίκευση την προηγουμένην πρότασιν, περί κέντρου βάρους παραβολικού τμήματος, εις το τραπεζοειδές παραβολικόν χωρίον το προκύπτον δια τομής του παραβολικού τμήματος υπ' ευθείας παραλλήλου προς την βάσιν (ακριβώς όπως λαμβάνεται εν τραπέζιον διά τομής τριγώνου υπ' ευθείας παραλλήλου προς την βάσιν του).

Ενώ με τα βιβλία του περί επιπέδων ισορροπιών ο μέγας Συρακούσιος εγένετο θεμελιωτής της Στερεοστατικής, εις ένα άλλο έργον του περί των εν ύδατι εφισταμένων η περί οχουμένων (βιβλία δύο) έθεσε τας βάσεις διά την μεθοδικήν ανάπτυξιν της Υδροστατικής και μάλλον θα ήτο ακριβέστερον να λεχθή ό,τι είπεν άλλοτε περί αυτού ο Lagrange, ότι δηλαδή ο Αρχιμήδης διά του εν λόγω έργου του^[2] εδίδαξε μίαν θεωρίαν επί της ισορροπίας των επιπλεόντων σωμάτων, εις την οποίαν οι νεώτεροι τίποτε δεν μετέβαλον, και πολύ ολίγα προσέθεσαν.

Και πράγματι δεν είναι δυνατόν να μη συμμερισθώμεν την γνώμην αυτήν του Lagrange, όταν η πασίγνωστος «αρχή του Αρχιμήδους» δεν λείπη σήμερον από κανένα εγχειρίδιον Φυσικής. Είναι άγνωστον, εάν η περίφημος αυτή «αρχή» υπήρξε το σημείον αφίξεως η το σημείον εκκινήσεως των σκέψεων, βάσει των οποίων ο Αρχιμήδης ανεκάλυψε τον δόλον πού είχε διαπράξει εις βάρος του τυράννου των Συρακουσών ο χρυσοχόος εκείνος, εις τον όποιον είχεν ανατεθή η κατασκευή στεφάνου εκ καθαρού χρυσού ^[3].

Της εν λόγω αρχής ο Αρχιμήδης υποδεικνύει, εις τα βιβλία πού ανεφέραμεν, μίαν σπουδαίαν και δυσκολωτάτην εφαρμογήν, προσδιορίζων τας συνθήκας ισορροπίας του στέρεου του προκύπτοντος εκ της τομής ενός ελλειπτικού παραβολοειδούς εκ περιστροφής υπό επιπέδου καθέτου επί τον άξονα, όταν το στερεόν τούτο βυθισθή εντός υγρού. Και η έρευνα αυτή εχρησίμευσεν επίσης ως κίνητρον και ως υπόδειγμα εις εκείνους, οι όποιοι βραδύτερον επεχείρησαν την λύσιν προβλημάτων του αυτού τύπου.

Η Ελληνική Ανθολογία, είναι μία συλλογή συγγραφείσα από κάποιον Μητρόδωρον (μεταξύ τέλους του V αιώνος και άρχων του VI αιώνος μ.Χ.) με τον αξιέπαινον σκοπόν να προσφέρη εις τους συμπατριώτας του ένα σύνολον ελκυστικών αριθμητικών προβλημάτων ποικίλου περιεχομένου, χωρίς όμως την αξίωσιν της παροχής ηγγυημένων ιστορικών πληροφοριών. Άλλωστε τα δεδομένα του ανωτέρω προβλήματος έχουν τόσον επιτυχώς συνδυασθή, ώστε να δίδουν πιστευτήν εικόνα των παραδοξοτήτων της ανθρώπινης ζωής.

Αλλά το ωραιότερον και δυσκολώτερον εκ των προβλημάτων των περιεχομένων εις την περί ης ο λόγος συλλογήν (τόσον δύσκολον εις την λύσιν και κατανόησίν του, ώστε απεκλείσθη από τάς πρώτας εκδόσεις) είναι το αποδιδόμενον εις τον Αρχιμήδη «βοεικόν πρόβλημα», αποσταλέν υπό τούτου προς τον επιστήθιον φίλον του Ερατοσθένην τον Κυρηναίον. Θεωρούμεν επιβαλλομένην υποχρέωσιν ν' αναφέρωμεν εδώ την πλήρη εκφώνησιν του προβλήματος :

Πληβὺν Ἠελίοιο βοῶν, ὦ ξεῖνε, μέτρησον
φροντίδ' ἐπιστήσας, εἰ μετέχεις σοφίης,
πόσση ἄρ' ἐν πεδίοις Σικελῆς ποτ' ἐβόσκετο νήσου
Θρινακίης τετραχῆ στίφεα δασσαμένη
5
χροιὴν ἀλάσσοντα· τὸ μὲν λευκοῖο γάλακτος,
κυανέωι δ' ἕτερον χρώματι λαμπόμενον,
ἄλλο γε μὲν ξανθόν, τὸ δὲ ποικίλον. Ἐν δὲ ἑκάστως
στίφει ἔσαν ταῦροι πλήθεσι βριθόμενοι
συμμετρίης τοιῆσδε τετευχότες· ἀργότριχας μὲν
10
κυανέων ταύρων ἡμίσει ἠδὲ τρίτω
καὶ ξανθοῖς σύμπασιν ἴσους, ὦ ξεῖνε, νόησον,
αὐτὰρ κυανέους τῶ τετράτω τε μέρει
μικτοχρόων καὶ πέμπτω, ἔτι ξανθοῖσί τε πᾶσιν.
Τους δ' ὑπολεπτομένους ποικιλόχρωτας ἄθρει
15
ἀργεννῶν ταύρων ἕκτω μέρει ἑβδομάτως τε
καὶ ξανθοῖς αὐτοὺς πᾶσιν ἰσαζομένους.
Θηλείαισι δὲ βουσὶ τάδ' ἔπλετο· λευκότριχες μὲν
ἦσαν συμπάσης κυανέης ἀγέλης
τῶι τριτάτω τε μέρει καὶ τετράτω ἀτρεκὲς ἶσαι·
20
αὐτὰρ κυάνεαι τῶι τετράτω τε πάλιν
μικτοχρόων καὶ πέμπτωι ὁμοῦ μέρει ἰσάζοντο
σὺν ταύροις πάσαις εἰς νομὸν ἐρχομέναις.
Ξανθοτρίχων δ' ἀγέλης πέμπτω μέρει ἠδὲ καὶ ἕκτω
ποικίλαι ἰσάριθμον πλήθος ἔχον τετραχῆς.
25
Ξανθαὶ δ' ἠριθμεῦντο μέρους τρίτου ἡμίσει ἶσαι
ἀργεννῆς ἀγέλης ἐβδομάτωι τε μέρει.
Ξεῖνε, σὺ δ' Ἠελίοιο βόες πόσαι ἀτρεκὲς εἰπών,
χωρὶς μὲν ταύρων ζατρεφέων ἀριθμόν,
χωρὶς δ' αὖ θήλειαι ὅσαι κατὰ χροιὰν ἕκασται,
30
οὐκ ἄιδρίς κα λέγοι' οὐδ' ἀριθμῶν ἀδαής,
οὐ μὴν πώ γε σοψοῖς ἐναρίθμιος. Ἀλλ' ἴθι φράζευ
καὶ τάδε πάντα βοῶν Ἠελίοιο πάθη.
Ἀργότριχες ταῦροι μὲν ἐπεὶ μιξαίατο πληθὺν
κυανέοις, ἵσταντ' ἔμπεδον ἰσόμετροι
35
εἰς βάθος εἰς εὖρός τε, τὰ δ' αὖ περιμήκεα πάντη
πίμπλαντο πλίνθου Θρινακίης πεδία.
Ξανθοὶ δ' αὖτ' εἰς ἐν καὶ ποικίλοι ἀθροισθέντες
ἵσταντ' ἀμβολάδην ἐξ ἑνός ἀρχόμενοι
σχῆμα τελειοῦντες τὸ τρικράσπεδον οὔτε προσόντων
40
ἀλλοχρόων ταύρων οὔτ' ἐπιλειπομένων.
Ταῦτα συνεξευρὼν καὶ ἐνὶ πραπίδεσσιν ἀθροίσας
καὶ πληθέων ἀποδούς, ξεῖνε, τὰ πάντα μέτρα
ἔρχεο κυδιόων νικηφόρος ἴσθι τε πάντως
κεκριμένος ταύτηι γ' ὄμπνιος ἐν σοφίης.
 

(Το πλήθος των βοών του Ηλίου υποτίθεται διηρημένον εις αγέλας ταύρων και αγελάδων διακρινομένων κατά τεσσάρας χρωματισμούς. Ο εις χρωματισμός είναι λευκός, ο άλλος κυανούς, ο τρίτος ξανθός και ο τέταρτος ανάμικτος. Όταν λέγουν οι αρχαίοι κυανούς εννοούν χρώμα πλησιάζον προς το μαύρον.

 Μέτρησον, ω ξένε, το πλήθος των βοών του Ηλίου, αφού καταβάλης προσεκτικήν σκέψιν, εάν είσαι μέτοχος σοφίας, πόσον λοιπόν εις τας πεδιάδας της σικελικής νήσου Θρινακίας έβοσκε, διηρημένον εις τέσσαρας αγέλας, εκάστη των όποιων είχε διαφορετικόν χρώμα. Η μία μεν αγέλη έλαμπεν έχουσα λευκόν ωσάν γάλα χρώμα, η δε άλλη έχουσα χρώμα κυανούν, η τρίτη είχε χρώμα ξανθόν, η δε άλλη χρώμα ανάμικτον. Εις εκάστην αγέλην υπήρχον ταύροι ανερχόμενοι εις αριθμόν πολύ μεγάλον, διαμοιρασμένοι κατά την ακόλουθον συμμετρίαν. Φαντάσου, ω ξένε, ότι οι λευκότριχες ταύροι ήσαν ίσοι κατά τον αριθμόν με το ήμισυ των κυανών ταύρων ηυξημένον κατά το τρίτον και συγχρόνως με τον συνολικόν αριθμόν των ξανθών. Οι κυανοί αφ' έτερου ήσαν κατά τον αριθμόν ίσοι με το τέταρτον και πέμπτον μέρος των αναμίκτου χρώματος και επί πλέον με τον συνολικόν αριθμόν των ξανθών. Τους δε υπολειπρμένους ανάμικτου χρώματος ταύρους φαντάζου ως εξισουμένους  κατά τον αριθμόν με το έκτον και έβδομον μέρος των λευκών και με τον συνολικόν αριθμόν των ξανθών. Ως  προς  τας  αγελάδας δε υπήρχον αι ακόλουθοι σχέσεις. Αι λευκαί  αγελάδες ήσαν  κατά τον αριθμόν ακριβώς ίσαι με το τρίτον και το τέταρτον μέρος όλης της κυανής αγέλης Αι δε κυαναί ήσαν ίσαι κατά τον αριθμόν με το τέταρτον και πέμπτον μαζί μέρος των εχουσών ανάμικτον χρωματισμόν, όταν ήρχοντο  όλαι μαζί  με τους  ταύρους  εις την  βοσκήν. Αι αναμίκτου δε χρωματισμού αγελάδες είχον αριθμόν ισάριθμον και οπό τα τέσσαρα  μέρη, με το πέμπτον και  έκτον μέρος της αγέλης των ξανθοτρίχων. Αι δε ξανθαί κατά την αρίθμησιν ευρίσκοντο ίσαι με το ήμισυ του τρίτου μέρους ηυξημένου κατά το έβδομον μέρος της αγέλης των λευκών. Συ δε, ω ξένε, αν μου είπης με ακρίβειαν πόσοι ήσαν οι βόες του Ηλίου, χωριστά πόσοι ήσαν κατά τον αριθμόν οι καλοθρεμμένοι ταύροι, χωριστά δε πάλιν πόσαι ήσαν αι αγελάδες εκάστου χρώματος, δεν θα χαρακτηρίζεσαι ως ανίδεος και  ως μη έχων  γνώσιν  των  αριθμών. Αλλά δεν θα είναι δυνατόν να  συγκαταριθμηθής ακόμη με τους σοφούς. Έλα λοιπόν σκέψου και τας  ακολούθους μεταξύ των βοών του  Ηλίου (αριθμητικάς)  σχέσεις. Όταν οι λευκότριχες ταύροι ανεμίγνυον το πλήθος των με το πλήθος των κυανών, ίσταντο εις ένα συμπαγή σχηματισμόν, όστις είχε το αυτό  μέτρον και κατά τα βάθος και  κατά το πλάτος, αι  δε πεδιάδες αι απέραντοι της Θρινακίας εγέμιζαν εξ ολοκλήρου από το τετράγωνον αυτό. Από το άλλο δε μέρος οι ξανθοί  και οι ανάμικτου χρώματος συναθροιζόμενοι μαζί, εστέκοντο τοιουτοτρόπως, ώστε να αποτελούν, αποτελούμενης της πρώτης γραμμής από ένα, βαθμηδόν το τρίπλευρον σχήμα, χωρίς να είναι παρόντες και χωρίς να είναι απόντες οι ταύροι των άλλων χρωματισμών. Αν αυτά τα εύρης και τα συμπεριλάβης μέσα εις την σκέψιν σου, και εκφράσης όλα τα μέτρα των πληθών, ω ξένε, άπελθε υπερηφανευόμενος ότι ανεδείχθης νικητής και να γνωρίζης ότι έχεις κριθή τέλειος εις αυτήν την σοφίαν.)

Δια να εκτιμήσωμεν τον βαθμόν της δυσκολίας του προβλήματος τούτου ας σημειωθή ότι, αν παραστήσωμεν με υ, χ, y, z τους αριθμούς των ταύρων και υ', x', y', z', εκείνους των αγελάδων εκάστης ομάδος, αι συνθήκαι του προβλήματος μεταφράζονται εις τας ακολούθους εξισώσεις:

Επειδή οι άγνωστοι πρέπει να έχουν ακεραίας τιμάς, εκ των επτά πρώτων εξισώσεων συνάγεται ότι αι εν λόγω τιμαί πρέπει να είναι της, μορφής:

υ = 10366482 λ   υ' = 7206360 λ

x = 7460514 λ    x'= 4893246 λ

y = 4069197 λ    y'= 5439213 λ

z = 7358060 λ    z' =3515820 λ

Αν λάβωμεν υπ' όψιν  την προτελευταίαν  συνθήκην του   προβλήματος, βλέπομεν ότι ο λ πρέπει να έχη την μορφήν 445•749ξ².

Τέλος η τελευταία συνθήκη, αν θέσωμεν 2q+l = t, 2.4657 ξ = υ, άγει εις την ακόλουθον σχέσιν μεταξύ t και υ:

t²—4729494 u² = l.

Η σχέσις αύτη ανήκει εις την κατηγορίαν των εξισώσεων, αι οποίαι κοινώς, καίτοι ατόπως, ονομάζονται «εξισώσεις του Pell». Πρόκειται τώρα να ευρεθή μία λύσις τοιαύτη, ώστε το u να είναι πολλαπλάσιον του 2^.4657. Εις την ελαχίστην των λύσεων τούτων, αντιστοιχεί ένας αριθμός βοών του Ηλίου εκφραζόμενος από τον αριθμόν 7766 ακόλουθούμενον υπό 206541 μηδενικών και δια να γράψωμεν τας τιμάς όλων των αγνώστων του προβλήματος — υπολογίζοντες 2500 ψηφία ανά σελίδα — θα εχρειάζετο να γεμίσωμεν ένα τόμον 660 σελίδων 8ου σχήματος ^[4].

Από το σύντομον αυτό διάγραμμα της λύσεως, η οποία ουδείς  θα τολμήση να ισχυρισθή ότι υπερέβαινε τας δυνάμεις ενός Αρχιμήδους, προκύπτει πόσον εξέχουσα ήτο η σημασία του προβλήματος και πόσον δικαιολογημένη ήτο η υπό των αρχαίων χρησιμοποίησες της φράσεως «βοεικόν πρόβλημα», προκειμένου να χαρακτηρίσουν γενικώς οιονδήποτε ζήτημα παρουσιάζον απελπιστικήν δυσκολίαν.

Τοιαύτης φύσεως πρόβλημα, προστιθέμενον εις τας άλλας ιστορικάς πληροφορίας πού έδωσα μεν σχετικώς με την έκτασιν της Αριθμητικής επιστήμης των Ελλήνων,  δεν αποδεικνύει  τίποτε άλλο παρά ότι ο λαός αυτός, αν και κατέστη κυρίως διάσημος δια την φυσικήν του ροπήν προς την γεωμετρίαν και δια τον όγκον των ανακαλύψεων, τας οποίας επραγματοποίησεν εις τον τομέα τούτον, εν τούτοις δεν ήτο αδιάφορος προς την έρευναν των ιδιοτήτων των αριθμών, ούτε απόστρεφε την προσοχήν του από προβλήματα ικανά να τρομοκρατήσουν τον δεινότερον υπολογιστήν. Δια τούτο η γνώμη, ότι τάχα οι Έλληνες έπασχον από μίαν ακατανίκητον αρνητικήν διάθεσιν προς την αριθμητικήν, πρέπει να θεωρήται μόνον ως προκατάληψις, απορρέουσα από παχυλήν άγνοιαν των όσων αποδεικνύουν από συμφώνου αδιαφιλονίκητα ιστορικά δοκουμέντα και κατά συνέπειαν μία τοιαύτη προκατάληψις πρέπει το ταχύτερον να καταπολεμηθή ως αβάσιμος.

Εν άλλο μικρόν έργον του Αρχιμήδους, περισωθέν, υπό τον τίτλον Ψαμμίτης το είχεν αφιερώσει εις τον βασιλέα Γέλωνα. Το έργον αυτό φέρεται εις την ελληνικήν, εις δε τας πρώτας λατινικός μεταφράσεις απεδόθη με τον τίτλον De numero arena ή Arenarius.

Η αιτιολογία του περιέργου αυτού τίτλου έγκειται εις το γεγονός, ότι εις το έργον, περί του οποίου πρόκειται, ο μέγας Συρακούσιος έθεσεν ως σκοπόν ν' απόδειξη αβάσιμον τον ισχυρισμόν ότι ο αριθμός των κόκκων της άμμου, πού υφίστανται εις τον κόσμον, ως άπειρος, δεν δύναται να εκφρασθή με τα εν χρήσει αριθμητικά σημεία. Διά να φθάση εις τον σκοπόν ο Αρχιμήδης αναλαμβάνει ν' απόδειξη ότι, αντιθέτως, είναι δυνατόν να παρασταθή γραφικώς ο αριθμός των κόκκων της άμμου, η οποία πληροί μίαν σφαίραν ομόκεντρον της γης και φθάνουσαν μέχρι των απλανών αστέρων, σφαίραν η οποία (όπως αποδεικνύει) έχει διάμετρον μη υπερβαίνουσαν τα 10¹⁰ στάδια.

Αφού θέσει προηγουμένως μερικάς εννοίας και ιδέας αστρονομικού χαρακτήρος, προβαίνει κατόπιν εις την παρατήρηση ότι εδόθησαν ονό­ματα εις τους αριθμούς τους μη υπερβαίνοντας την μυριάδα και ότι δι' αριθμούς μεγαλύτερους δεν γίνεται τίποτε άλλο παρά να επαναλαμβάνεται μία μυριάς μέχρι μυρίων μυριάδων. Ας ονομασθούν λοιπόν «πρώτοι αριθμοί» όλοι οι ούτω προκύπτοντες

και «μονάς των δευτέρων αριθμών» η μυριάς μυριάδων του μεγίστου πρώτου αριθμού. Με την νέαν αυτήν μονάδα ας αριθμήσωμεν κατά δεκάδας, εκατοντάδας, χιλιάδας και μυριάδας μέχρι μιας μυριάδος μυριάδων (10⁸). Μία μυριάς μυριάδων μονάδων δευτέρων αριθμών ήτοι ο αριθμός 10^3•8, έστω «μονάς των τρίτων αριθμών». Και με την ιδίαν μέθοδον προχωρούμεν μέχρις ότου φθάσωμεν τον αριθμόν

, 

δηλαδή τον αριθμόν, ο όποιος εκφράζεται γραπτώς υπό της μονάδος ακολουθούμενης υπό 800 εκατομμυρίων μηδενικών.

Εξακολουθεί ο Αρχιμήδης παρατηρών ότι, αν και το πλήθος των αριθμών τούτων είναι πλουσιώτατα επαρκές διά να επιτύχη τον προταθέντα σκοπόν, είναι μολοντούτο εύκολον να προχωρήσωμεν αναλόγως, πολύ περισσότερον. Πράγματι όλοι οι αριθμοί πού δεν υπερβαίνουν τον

 ας ονομασθούν «αριθμοί πρώτης περιόδου» και εις τον τελευταίον της περιόδου ταύτης ας δοθή το όνομα «μονάς των πρώτων αριθμών της δευτέρας περιόδου». Αριθμούμεν τώρα με αυτούς μέχρις ότου φθάσωμεν τον αριθμόν

και ας κληθή ούτος «μονάς των δευτέρων αριθμών τής δευτέρας περιόδου». Προχωρούμεν αναλόγως φθάνοντες διαδοχικώς τας μονάδας

μέχρι τού αριθμού  

Τοιουτοτρόπως θα έχουν ληφθή όλοι οι αριθμοί της β' περιόδου. Ο τελευταίος τούτων θα εκφράζεται υπό της μονάδος ακολουθούμενης υπό 1600 εκατομμυρίων μηδενικών.

Είναι δυσκολώτατον να λάβωμεν εμπειρικήν εικόνα του μεγέθους τοιούτου αριθμού. Δια να σχηματίσωμεν κάπως μίαν ιδέαν, θα ήτο ίσως σκόπιμον να λάβωμεν υπ' όψιν τάς ακολούθους σκέψεις.

α) Αν υποθέσωμεν ότι ένα ψηφίον κατέχει γραμμικώς εις τον χάρτην διάστημα 2 mm, διά να γράψωμεν 1600 εκ. μηδενικά, το ένα κατόπιν του άλλου, χρειάζεται μία ταινία μήκους 3.200.000 μέτρων ή 3.200 χιλιομέτρων, η οποία αντιπροσωπεύει διάστημα διανυόμενον από ταχύτατον συρμόν εις 32 ώρας.

β) Αν, διά ν' αποφύγωμεν την χρήσιν μιας τόσον δύσχρηστου ταινίας, προτιμήσωμεν να καταχωρήσωμεν τον αριθμόν εις βιβλίον, θα παρατηρήσωμεν ότι οι συνήθεις πίνακες λογαρίθμων περιέχουν εις εκάστην σελίδα 50 γραμμάς, εκάστη των οποίων περιέχει 50 ψηφία, όθεν εις εκάστην σελίδα εισέρχονται 2500 ψηφία. Διά να γράψωμεν λοιπόν τον αριθμόν περί ου πρόκειται χρειάζονται 640.000 σελίδες, δηλαδή 1280 τόμοι των 500 σελίδων έκαστος μία ολόκληρος βιβλιοθήκη!

γ) Λαμβάνοντες υπ' όψιν, ότι διά να γράψωμεν ένα ψηφίον χρειαζόμεθα κάτι ολιγώτερον του ενός δευτερολέπτου, εις μίαν ώραν (3600 sec) θα ημπορέσωμεν να γράψωμεν περίπου 4000 ψηφία και 40000 εις μίαν ημέραν δεκαώρου συνεχούς εργασίας. Όθεν διά να γράψωμεν τον περί ου ο λόγος αριθμόν θα χρειασθώμεν 40000 ημέρας, περισσότερος δηλαδή μιας ζωής πλήρους δραστηριότητος!

Ο Αρχιμήδης σταματά εις τον τελευταίον αριθμόν της δευτέρας περιόδου, χωρίς να παράλειψη την παρατήρησιν, ότι η υπ' αυτού υποδεικνυόμενη μέθοδος γενέσεως αριθμών ολονέν μεγαλυτέρων δύναται να εφαρμοσθή απεριορίστως, όπως είναι εύκολον να πεισθή οιοσδήποτε. Προς διευκόλυνσιν του υπολογισμού με τας νέας αριθμητικάς οντότητας του Αρχιμήδους, ούτος αποκαθιστά το θεώρημα, το όποιον εκφράζομεν σήμερον διά του τύπου :

 

10^m • 10ⁿ = 10^m+n

όπου m, η φυσικοί αριθμοί. Με την βοήθειαν του θεωρήματος τούτου και όλων των άλλων αστρονομικών και αριθμητικών αρχών, τας οποίας προτάσσει, ο μέγας μαθηματικός φθάνει εις το συμπέρασμα ότι υφίσταται ένας αριθμός, ουχί μεγαλύτερος του 10⁶³, ικανός να παραστήση το πλήθος των κόκκων τής άμμου, πού θα ήδύναντο να καταλάβουν τον χώρον μιας σφαίρας ομοκέντρου προς την γήν, εκτεινομένης μέχρι των απλανών αστέρων.

Και πράγματι εκείνος ο όποιος θα διεξέλθη το πρωτοτυπώτατον αυτό έργον του Αρχιμήδους δεν θα δυνηθή ν' αρνηθή ότι ούτος επέτυχε τον προκαθορισθέντα μακρυνόν στόχον. Αλλά συγχρόνως επέτυχε κάτι πολύ περισσότερον τούτου και καλύτερον. Με το ευφυέστατον αυτό έργον έδειξεν εις τους ομοεθνείς του, οι όποιοι εκυριαρχούντο από ακατανίκητον προκατάληψιν προς τους μεγάλους αριθμούς, ότι και οι αριθμοί αυτοί δύναν­ται να υποβληθούν εις τους ιδίους χειρισμούς, όπως και οι λοιποί της φυσικής σειράς. Επέτυχε δε τοιουτοτρόπως να στρέψη την προσοχήν των συγχρόνων του προς την αριθμητικήν αντίληψιν του απείρως μεγάλου, όπως ακριβώς με την «μέθοδον τής εξαντλήσεως» επέτυχε να διάλυση τας προκαταλήψεις των εναντίον του απείρως μικρού.

Ο Ψαμμίτης είναι έργον τόσον στέρεας δομής και τοιαύτης δυνάμεως, ώστε σχεδόν δεν αφίνει τίποτε να επιθυμήση κανείς. Ακόμη και εκείνοι, οι όποιοι θα επεχείρουν να σταχυολογήσουν εις τον αγρόν τον όποιον εθέρισεν ο Αρχιμήδης, θα επείθοντο πολύ γρήγορα ότι οι κόποι των ματαίως έπρεπε ν’ αναμένουν την παραμικράν ανταπόδοσιν.

Εδώ είναι μάλλον κατάλληλος η στιγμή να ομιλήσωμεν εις κάποιαν έκτασιν διά τας μεθόδους, τας οποίας μετήρχετο ο Αρχιμήδης, πρώτον διά την ανακάλυψιν και έπειτα διά την απόδειξιν  των θεωρημάτων του.

Ως προς την μέθοδον της αποδείξεως, έχομεν να παρατηρήσωμεν, ότι αύτη χαρακτηρίζεται από ευρυτάτην χρήσιν της γεωμετρικής άλγεβρας, εις την οποίαν ο Αρχιμήδης έδωσε μορφήν κομψοτέραν και ισχυροτέραν της απαντωμένης εις τον Ευκλείδη.

Χαρακτηρίζεται ακόμη από ευρείαν χρήσιν της υπό των αρχαίων καλούμενης «νεύσεσως», δηλαδή γεωμετρικής πράξεως αποσκοπούσης εις την τοποθέτησιν ευθυγράμμου τμήματος κατά τοιούτον τρόπον, ώστε τα άκρα του να κείνται επί δύο δοθεισών γραμμών, η δε ευθεία εις ην ανήκει το τμήμα να διέρχεται από δεδομένον σημείον. Αξιοσημείωτον είναι ότι ο Αρχιμήδης επικαλείται την «νεύσιν» ακόμη και όταν είναι αδύνατος η πραγματοποίησις αυτής διά του κανόνος και του διαβήτου, πράγμα επιδεχόμενον προφανώς την ερμηνείαν ότι ο ίδιος δεν διετήρει επιφυλάξεις ως προς την μηχανικήν εκτέλεσιν της νεύσεως μέσω κανόνος φέροντος επ' αυτού τα σημεία τα παριστώντα τα άκρα του δοθέντος ευθυγράμμου τμήματος.

Τέλος ο Αρχιμήδης εφήρμοσεν εις ευρείαν κλίμακα τας υπό του Ευδόξου αναπτυχθείσας πρωτοτύπους ιδέας, τας οποίας εφήρμοσε μετ' επιτυχίας και ο Ευκλείδης, διά τον υπολογισμόν εμβαδών και όγκων, χωρίς την χρήσιν εκπεφρασμένων μεθόδων ολοκληρωτικού λογισμού. Προσέθεσε δε εις την μέθοδον του Ευδόξου και την ιδικήν του πρωτότυπον συμβολήν, δηλαδή την χρήσιν του ζυγού, όπως είδομεν ήδη εις τα περί τετραγωνισμού της παραβολής.

Επειδή πλείστοι από τους αποδεικτικούς συλλογισμούς του Αρχιμήδους, αν και προκαλούν τον θαυμασμόν διά την πρωτοτυπίαν των, είναι τεχνασματικοί και δεν στερούνται περιπλοκών, ηγέρθη εις πολλούς η βάσιμος υπόνοια ότι οι αποδεικτικοί του συλλογισμοί δεν ήσαν εκείνοι, πού ωδήγησαν αρχικώς τον Αρχιμήδη εις την ανακάλυψιν των αληθειών, πού τον  κατέστησαν  διάσημον εις όλόκληρον τον κόσμον.

Η εικασία αυτή εύρε πράγματι την φαεινοτέραν δικαίωσιν, όταν, κατά τας αρχάς του αιώνος, ανεκαλύφθη εις μίαν βιβλιοθήκην της Κωνσταντινουπόλεως ένα παλίμψηστον, εις το όποιον φέρεται εγγεγραμμένον σημαντικόν απόσπασμα έργου του Αρχιμήδους, υπό τον τίτλον «Η έφοδος». Το έργον τούτο έχει μεθοδολογικόν χαρακτήρα και μεταξύ άλλων καθιερώνει την διάκρισιν μεταξύ «μεθόδου ανακαλύψεως» και «μεθόδου αποδείξεως» των γεωμετρικών αληθειών.

Χωρίς επιφυλάξεις ο Αρχιμήδης διατυπώνει την άποψιν, ότι ενώ η σειρά των συλλογισμών, διά των οποίων αποδεικνύεται ένα θεώρημα, πρέπει να είναι απηλλαγμένη παντός στοιχείου μη ανήκοντος εις την επιστήμην του διαστήματος, ο διεξάγων μίαν επιστημονικήν έρευναν είναι ελεύθερος να χρησιμοποίηση οιονδήποτε μέσον ικανόν να τον οδηγήση ασφαλέστερα εις τον σκοπών. Σοφή συμβουλή, η οποία ακόμη και σήμερον θα ηδύνατο να βοηθήση όλους τους επιμένοντας να πηλοβατούν εις μίαν άγονον τυπικότητα και σχολαστικότητα.

Τοιουτοτρόπως ο Αρχιμήδης μας επιτρέπει να εγγίσωμεν διά της χειρός την ευστροφίαν που μεταχειρίζεται εις πολλάς περιπτώσεις, ειδικώτερον μάλιστα εις τον προσδιορισμόν του όγκου κυλινδρικού όνυχος ή του κοινού όγκου δύο ορθών κυκλικών κυλίνδρων της αυτής διαμέτρου, αλληλοτομούντων κατ' άξονα υπό ορθήν γωνίαν. Ο όγκος ούτος είναι, όπως αποδεικνύει ο Αρχιμήδης, ίσος προς τα 2/3 του κύβου του έχοντος πλευράν την κοινήν διάμετρον των κυλίνδρων ^[5].

Τα έργα του Αρχιμήδους, τα όποια εξητάσαμεν μέχρι τούδε εν συντομία, έφθασαν μέχρις ημών σχεδόν ολόκληρα, έστω και αν όχι όλα εις την αρχικήν των γλώσσαν, αποδίδονται όμως ακόμη εις αυτόν πολλά άλλα, περί των οποίων θα κάμωμεν συντομωτάτην μνείαν.

Λέγεται ότι έγραψε μίαν πραγματείαν περί κωνικών τομών, διά την συγγραφήν της οποίας άλλωστε ήτο αρμοδιώτατος, λαμβανομένης υπ' όψει της βαθείας γνώσεως των ιδιοτήτων των γραμμών τούτων, της αποκαλυπτόμενης εις άλλα έργα του. Έγραψεν ακόμη ένα έργον περί ημικανονικών πολυέδρων, ήτοι σχημάτων του χώρου περιοριζόμενων υπό κανονικών πολυγώνων διαφόρων ειδών. Διά μέσων αγνώστων εις ημάς, προσδιώρισε τον αριθμόν αυτών εις δεκατρία, ωθηθείς πιθανώς από την εξέτασιν των δύο γνωστών εις τον Πλάτωνα.

Υπό το όνομα του Αρχιμήδους φέρεται επίσης μία συλλογή προτάσεων στοιχειώδους γεωμετρίας, περιελθούσα εις ημάς μέσω των Αράβων, οι όποιοι πιθανώς ήντλησαν το περιεχόμενον εκ διαφόρων πηγών. Διά να δώσωμεν μίαν ιδέαν του περιεχομένου του βιβλίου τούτου, γνωστού ύπό τον τίτλον Λήμματα^[6], θα αναφέρωμεν τα δύο ακόλουθα θεωρήματα, αφορώντα νέα επίπεδα σχήματα, περικλεισμένα υπό κυκλικών τόξων, και τα όποια, όπως οι μηνίσκοι του Ιπποκράτους, έχουν εμβαδά εκφραζόμενα κατά τρόπον αξιοσημείωτον.

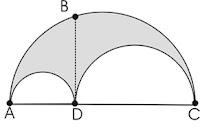
α) «Εάν επί της διαμέτρου AC ημικυκλίου (σχ. 2) ληφθή σημείον D και γράφουν από των τμημάτων της διαμέτρου δύο ημικύκλια εντός, από του ληφθέντος δε σημείου υψωθή κάθετος επί την διάμετρον μέχρι της ημιπεριφέρειας, το σχήμα το περιεχόμενον υπό των τριών τόξων — καλούμενον άρβηλον — ισούται με κύκλον του οποίου διάμετρος είναι η υψωθείσα κάθετος DB ».

 

Σχήμα 2

Σχήμα 3

β) «Εάν εις ημικύκλιον (σχ. 3) ληφθούν δύο ίσα τμήματα ΑΕ και GC από των άκρων της διαμέτρου AC και από τούτων γράφουν ημικύκλια εντός,  γραφή δε και από του υπολοίπου τμήματος EG ημικύκλιον εκτός, ο κύκλος του οποίου διάμετρος είναι το άθροισμα των ακτινίων του ληφθέντος ημικυκλίου και του έκτος, ισούται προς το εμβαδόν του σχήματος του περικλεισμένου υπό των τόξων όλων των ημικυκλίων —γνωστού με το όνομα   σάλινον ^[7] ».

Μία μονογραφία του Συρακούσιου μαθηματικού επί του επταγώνου εθεωρείτο μέχρι του τέλους του Χ αιώνος ως απολεσθείσα. Ευρέθησαν όμως διάφορα αντίγραφα εις την αραβικήν, ένα των οποίων, οφειλόμενον εις τον Tabit ibn Quorra (836-901), είδε το φώς της δημοσιότητος εις γερμανικήν γλώσσαν. 'Εξ αυτού διδασκόμεθα μίαν κομψή ν πρότασιν, σχετικήν προς το κανονικόν επτάγωνον, την οποίαν θεωρούμεν σκόπιμον ν' αναφέρωμεν εδώ. «Δίδεται (σχ. 4) η ευθεία ΑΒ, εφ' ης λαμβάνομεν δύο σημεία C και D τοιαύτα, ώστε να έχωμεν :

 Σχήμα4

AD-CD = DB²

CD-DB = AC²

Τα τμήματα AC, DB, προκύπτουν μεγαλύτερα του CD, ώστε επιτρέπουν την κατασκευήν ενός τριγώνου CHD τοιούτου, ώστε CH = AC, DH = BD. Περιγράφομεν τώρα εις το τρίγωνον ΑΗΒ περιφέρειαν Γ, και προεκτείνομεν τας πλευράς HC, HD μέχρι της περιφερείας, τεμνόμενης αντιστοίχως εις Ζ καί Ε. Έστω Τ το κοινόν σημείον των ευθειών ΒΖ, HE. Τα 4 σημεία C, Τ, Β, Η είναι ομοκυκλικά, τα δε τρία τόξα της Γ περιφερείας ΒΗ, ΑΖ, ΖΕ προκύπτουν ίσα μεταξύ των, ενώ τα υπόλοιπα ΑΗ καί BE διπλάσια των πρώτων, ούτως ώστε τούτων διχοτομουμένων, η περιφέρεια Γ έχει διαιρεθή εις επτά ίσα μέρη ».

Οι ακόλουθοι του Μωάμεθ μας μετέδωσαν επίσης αρκετάς πληροφορίας αναφορικώς προς ένα παίγνιον, παιζόμενον, κατά εφεύρεσιν του Αρχιμήδους, με πλακίδια εξ ελεφαντοστού, σχήματος τριγωνικού και πολυγωνικού, καλούμενον δε συνήθως loculus Archimedius ή στομάχιον. Κάμνομεν απλώς μνείαν του παιγνιδιού τούτου, εν μέσω τόσων άλλων μηχανών πού επενόησεν ο ίδιος — χωρίς να δίδη δι' αυτάς μεγάλην σημασίαν, ενώ αντιθέτως αύται διήγειρον άμετρον θαυμασμόν εις τους συγχρόνους του — διότι εκείνος πού επιθυμεί να σχηματίση ακριβή αντίληψιν μιας τόσον εξεχούσης προσωπικότητος, ως ο Αρχιμήδης, δεν είναι θεμιτόν να παράλειψη καμμίαν από τας πολλάς απόψεις, υπό τας οποίας αύτη εμφανίζεται, μολονότι, αι πληροφορίαι τας οποίας εδώσαμεν αναφορικώς προς το καθαρώς μαθηματικόν έργον του, είναι επαρκείς διά να καταδείξουν πόσον δίκαιον είχεν ο G. Wallis λέγων ότι «ο Αρχιμήδης υπήρξεν άνήρ εκπληκτικής αγχινοίας, ο οποίος   έθεσε πρώτος τα θεμέλια σχεδόν όλων εκείνων των επινοήσεων, διά τας  οποίας καυχάται η εποχή μας ».

1.           Αν και δεν υπάρχη καμμία σχετική μαρτυρία, εν τούτοις μας φαίνεται ευλογωτάτη η σκέψις, ότι ενδέχεται η γενική έννοια των πολικών συντεταγμένων να έλκη την καταγωγήν της από την ανωτέρω εργασίαν του Αρχιμήδους και ότι εκ της μελέτης ταύτης ωδηγήθησαν πιθανώς εις την εισαγωγήν, ως βοηθητικού μεγέθους προς χάραξιν των εφαπτόμενων, της πολικής υφαπτομένης και συνεκδοχικώς και της, πολικής υποκαθέτου.

2.           Του έργου τούτου εσώζετο μόνον η λατινική μετάφρασις, εσχάτως όμως ανεκαλύφθη και το ελληνικόν κείμενον εις ένα παλίμψηστον υφιστάμενον εις την Ιερουσαλήμ. Η μετάφρασις, η όποια υπήρχε προηγουμένως, ήτο έργον του G. de Moerbeke, και έκδοσις του Ν. Tartaglia.

3.           Ο Ρωμαίος μηχανικός και αρχιτέκτων Βιτρούβιος (περί το 25 π.Χ.) εις το περίφημον, εκ δέκα βιβλίων, έργον του De Architecture αναφέρει, σχετικώς με το περιστατικόν τούτο, τα εξής (Ι. IX, Κεφ. III) : «Ιέρων, ο άρχων της πόλεως των Συρακουσών, άποφασίσας να κατάθεση εις τον ναόν πολύτιμον στέφανον εκ καθαρού χρυσού, ως ανάθημα ευχαριστίας διά την ευημερίαν της πόλεως, ανέθεσε την κατασκευήν αυτού εις χρυσοχόον, εις τον όποιον και παρέδωσεν ωρισμένον βάρος καθαρού χρυσού. Ούτος παρέδωσε μετά τινα χρόνον εις τον βασιλέα τον στέφανον, επεξειργασμένον διά χειρών με μεγάλην τέχνην, εις βάρος δε ίσον προς το βάρος του χρυσού, τον όποιον παρέλαβε. Ηγέρθη όμως υπόνοια ότι αφηρέθη ένα μέρος εκ του χρυσού, αντίκατασταθέν υπό ίσου βάρους αργύρου. Ωργισμένος  ο   Ιέρων   με   την ίδέαν  ότι   ηπατήθη   και  μη   γνωρίζων  πώς   ν' αποδείξη την κλοπήν, παρεκάλεσε τον Αρχιμήδη να καταβάλη. πασαν δυνατήν προσπάθειαν προς ανακάλυψιν του δόλου. Ο τελευταίος εισελθών κατά τύχην ολίγον έπειτα εις λουτήρα, παρετήρησεν ότι όσον εβυθίζετο το σώμα του, τόσον μεγαλύτερα ποσότης ύδατος εξεχείλιζεν εκ του λουτήρος. Εμπνευσθείς τότε τον τρόπον άνακαλύψεως της νοθείας του στεφάνου εκυριεύθη από τόσην χαράν, ώστε εξελθών γυμνός εις τον δρόμον κατηυθύνετο εις την οικίαν του φωνάζων «εύρηκα, εύρηκα!»

4.           Δύναται να προστεθή ότι επειδή δεν αρκεί η χωρητικότης της Σικελίας να περιλάβη τοιούτον αριθμών ζώων, το βοεικόν πρόβλημα δεν οφείλεται εις έμπνευσιν υποκινηθείσαν εκ συνθηκών της πραγματικότητος.

5.           Ομιλούντες σύγχρονον μαθηματικήν γλώσσαν, θα ήτο δυνατόν να είπωμεν ότι πρόκειται περί του κοινού μέρους των δύο κυλίνδρων x² + y² = r², y² + z² = r², του οποίου ο όγκος δίδεται από το διπλούν ολοκλήρωμα:

6.    Τα Λήμματα εσώθησαν εις αραβικήν γλώσσαν, εκ της οποίας και μετεφράσθησαν εις την λατινικήν υπό τον τίτλον Liber Assuptorum, εξεδόθησαν δε το πρώτον εν Λονδίνω κατά το 1659 υπό του S. Foster. Βραδύτερον μετεφράσθησαν και εις άλλας γλώσσας. Εδημοσιεύθη διά πρώτην φοράν ελληνική μετάφρασις των Λημμάτων εις το Δελτίον της Ε.Μ.Ε. του έτους 1965, οφειλομένη εις τον καθηγητήν και Ιστορικόν της μαθηματικής επιστήμης κ. Ε. Σταμάτη, όστις μάλιστα δεν εφείσθη κόπων ν' ανακατασκευάση μετά θαυμαστής επιμελείας και να δημοσίευση παραλλήλως προς το νεοελληνικόν, και το αρχαίον, υπ' αυτού ανακατασκευασθέν κείμενον εις σικελικήν δωρικήν διάλεκτον (Δελτίον Ε.Μ.Ε, Νέα σειρά, 1965, Τόμος 6,11, σελ. 265-297).

7.    Σχετικώς προς την ονομασίαν σάλινον, ο καθηγητής κ. Ε. Σταμάτη φρονεί ότι πρόκειται περί λάθους κατά την αντιγραφήν και ότι η ελληνική λέξις ήτο σελήνιον, ήτοι μηνίσκος σελήνης, ούτω δε είχε διορθώσει το κείμενον και ο Isaac Barrow, ο καθηγητής του Isaac Newton. Κατά τον T.L.Heath (Introduction to the works of Archimedes,1897) η λέξις προήλθεν από εξελληνισμόν της λατινικής λέξεως salinum, noi σημαίνει αλατοδοχείον, και δεν οφείλεται εις τον Αρχιμήδη, άλλα εις μεταγενεστέρους αντιγραφείς.

Όσον αφορά την σημασίαν της λέξεως άρβηλος ή άρβηλον, ο Heath παραπέμπει εις σχόλια του Νικάνδορυ, γραμματικού, ποιητού και Ιατρού του Β' αιώνος π.Χ περιεχόμενα εις το έργον του Θ η ρ ι α κ ά 423 :   «άρβηλοι λέγονται τα κυκλοτερή σιδήρια, οις οι σκυτοτόμοι τέμνουσι και ξέουσι τα δέρματα».