G. LORIA
 Είναι βέβαιον
ότι αναμφισβήτητα επίσης δικαιώματα εις τον θαυμασμόν μας, όχι oλιγώτερα του Ιπποκράτους, κατέχει ο Αρχύτας o Ταραντίνος (428 - 365 π. Χ.), ο
τελευταίος των Πυθαγορείων (ultimus Pithagoreorum), ο όποιος υπό των συγχρόνων, αλλά και των
αμέσως μεταγενεστέρων των, περιγράφεται ως ο ιδεώδης τύπος του ελληνικού ανθρώπου
εν μέσω μιας εκφυλισθείσης γενεάς. Στρατηγός
συγκρίσιμος προς τους μέγιστους, ουδέποτε υπέστη το όνειδος της ήττης, φιλόσοφος και ηθικολόγος επιφανής, είχε την δόξαν να
ίδη τον Πλάτωνα μεταξύ των πολυαρίθμων άλλων μαθητών
του. Άριστος εργάτης της Αστρονομίας και της Μηχανικής, εθαυμάζετο
από τον Οράτιον, ο όποιος δεν παρέλειψε να μνημόνευση
εις στίχους το τραγικόν του τέλος κατά την διάρκειαν ενός ναυαγίου εις την Αδριατικήν
θάλασσαν :
Είναι βέβαιον
ότι αναμφισβήτητα επίσης δικαιώματα εις τον θαυμασμόν μας, όχι oλιγώτερα του Ιπποκράτους, κατέχει ο Αρχύτας o Ταραντίνος (428 - 365 π. Χ.), ο
τελευταίος των Πυθαγορείων (ultimus Pithagoreorum), ο όποιος υπό των συγχρόνων, αλλά και των
αμέσως μεταγενεστέρων των, περιγράφεται ως ο ιδεώδης τύπος του ελληνικού ανθρώπου
εν μέσω μιας εκφυλισθείσης γενεάς. Στρατηγός
συγκρίσιμος προς τους μέγιστους, ουδέποτε υπέστη το όνειδος της ήττης, φιλόσοφος και ηθικολόγος επιφανής, είχε την δόξαν να
ίδη τον Πλάτωνα μεταξύ των πολυαρίθμων άλλων μαθητών
του. Άριστος εργάτης της Αστρονομίας και της Μηχανικής, εθαυμάζετο
από τον Οράτιον, ο όποιος δεν παρέλειψε να μνημόνευση
εις στίχους το τραγικόν του τέλος κατά την διάρκειαν ενός ναυαγίου εις την Αδριατικήν
θάλασσαν :
 Είναι βέβαιον
ότι αναμφισβήτητα επίσης δικαιώματα εις τον θαυμασμόν μας, όχι oλιγώτερα του Ιπποκράτους, κατέχει ο Αρχύτας o Ταραντίνος (428 - 365 π. Χ.), ο
τελευταίος των Πυθαγορείων (ultimus Pithagoreorum), ο όποιος υπό των συγχρόνων, αλλά και των
αμέσως μεταγενεστέρων των, περιγράφεται ως ο ιδεώδης τύπος του ελληνικού ανθρώπου
εν μέσω μιας εκφυλισθείσης γενεάς. Στρατηγός
συγκρίσιμος προς τους μέγιστους, ουδέποτε υπέστη το όνειδος της ήττης, φιλόσοφος και ηθικολόγος επιφανής, είχε την δόξαν να
ίδη τον Πλάτωνα μεταξύ των πολυαρίθμων άλλων μαθητών
του. Άριστος εργάτης της Αστρονομίας και της Μηχανικής, εθαυμάζετο
από τον Οράτιον, ο όποιος δεν παρέλειψε να μνημόνευση
εις στίχους το τραγικόν του τέλος κατά την διάρκειαν ενός ναυαγίου εις την Αδριατικήν
θάλασσαν :
Είναι βέβαιον
ότι αναμφισβήτητα επίσης δικαιώματα εις τον θαυμασμόν μας, όχι oλιγώτερα του Ιπποκράτους, κατέχει ο Αρχύτας o Ταραντίνος (428 - 365 π. Χ.), ο
τελευταίος των Πυθαγορείων (ultimus Pithagoreorum), ο όποιος υπό των συγχρόνων, αλλά και των
αμέσως μεταγενεστέρων των, περιγράφεται ως ο ιδεώδης τύπος του ελληνικού ανθρώπου
εν μέσω μιας εκφυλισθείσης γενεάς. Στρατηγός
συγκρίσιμος προς τους μέγιστους, ουδέποτε υπέστη το όνειδος της ήττης, φιλόσοφος και ηθικολόγος επιφανής, είχε την δόξαν να
ίδη τον Πλάτωνα μεταξύ των πολυαρίθμων άλλων μαθητών
του. Άριστος εργάτης της Αστρονομίας και της Μηχανικής, εθαυμάζετο
από τον Οράτιον, ο όποιος δεν παρέλειψε να μνημόνευση
εις στίχους το τραγικόν του τέλος κατά την διάρκειαν ενός ναυαγίου εις την Αδριατικήν
θάλασσαν :
«Αρχύτα, εσύ, πού να μετράς τη γη,
τη
θάλασσα νογάς, την άπειρη άμμο,
λίγη
μονάχα σκόνη
κοντά
στο Λίντο - Μαρτίνο τώρα εσύ κρατάς·
ούτε
ωφελήθηκες, για να σωθής, από τη γη
τα
άστρα ακολουθώντας, στον Πόλο ν' ανεβής».
(Ωδή
28η του Ι Βιβλίου)
Εις την ιστορίαν των μαθηματικών τα ίχνη του
παρέμειναν από μίαν πνευματώδη λύσιν, πού έδωσεν εις το πρόβλημα του
διπλασιασμού του κύβου, στηριζόμενος εις την μέθοδον της αναγωγής του
Ιπποκράτους, δια της παρεμβολής δύο μέσων αναλόγων μεταξύ δύο δοθέντων μηκών.
Δια να χαρακτηρίσωμεν την μέθοδον πού επενόησεν ο Αρχύτας, ας θεωρήσωμεν
τας κατωτέρω επιφανείας, αι οποίαι εις ορθογώνιους καρτεσιανάς συντεταγμένος παρίστανται
από τας εξισώσεις :
Εκ τούτων η πρώτη παριστά ορθόν κυκλικόν
κύλινδρον παρά τον άξονα των z
με βάσιν κύκλον διαμέτρου α.
Η δευτέρα ορθόν κυκλικόν κώνον
με κορυφήν εις την αρχήν και άξονα τον άξονα των z. Ή τρίτη παριστά αμφοίσμα γεννώμενον εκ της περιφερείας
διαμέτρου α, περιστρεφόμενης περί μίαν εφαπτομένην της συμπίπτουσαν με
τον άξονα των z. Έστω P ένα
κοινόν ση μείον των επιφανειών τούτων — διάφορον της
αρχής — και ας θέσωμεν :
Τότε αι προηγούμενοι εξισώσεις γράφονται :
Εκ τούτων δε λαμβάνομεν :
Επειδή τώρα η θέσις του P είναι ωρισμένη, καθορίζονται αι
δύο μέσαι ανάλογοι u, ν
μεταξύ των a, b και αν
συνεπώς ληφθή b = a  , ο κύβος διπλασιάζεται.
Η ανωτέρω μέθοδος, τόσον ευφυής υφ' ην έννοιαν εκτίθεται,
δεν αποδεικνύει μόνον το εφευρετικόν δαιμόνιον του
Αρχύτα και την μεγάλην του οικειότητα με τα σχήματα
του χώρου, άλλα όταν αναλυθή εις τα επί μέρους
βήματα, μας οδηγεί επίσης εις το να εκτιμήσωμεν με ακρίβειαν τας μεγάλας προόδους,
τας οποίας είχεν επιτελέσει εις την Ελλάδα η γεωμετρία του επιπέδου και του
χώρου, κατά τον αιώνα πού ηκολούθησε τον θάνατον του Πυθαγόρου.
, ο κύβος διπλασιάζεται.
Η ανωτέρω μέθοδος, τόσον ευφυής υφ' ην έννοιαν εκτίθεται,
δεν αποδεικνύει μόνον το εφευρετικόν δαιμόνιον του
Αρχύτα και την μεγάλην του οικειότητα με τα σχήματα
του χώρου, άλλα όταν αναλυθή εις τα επί μέρους
βήματα, μας οδηγεί επίσης εις το να εκτιμήσωμεν με ακρίβειαν τας μεγάλας προόδους,
τας οποίας είχεν επιτελέσει εις την Ελλάδα η γεωμετρία του επιπέδου και του
χώρου, κατά τον αιώνα πού ηκολούθησε τον θάνατον του Πυθαγόρου.
 , ο κύβος διπλασιάζεται.
Η ανωτέρω μέθοδος, τόσον ευφυής υφ' ην έννοιαν εκτίθεται,
δεν αποδεικνύει μόνον το εφευρετικόν δαιμόνιον του
Αρχύτα και την μεγάλην του οικειότητα με τα σχήματα
του χώρου, άλλα όταν αναλυθή εις τα επί μέρους
βήματα, μας οδηγεί επίσης εις το να εκτιμήσωμεν με ακρίβειαν τας μεγάλας προόδους,
τας οποίας είχεν επιτελέσει εις την Ελλάδα η γεωμετρία του επιπέδου και του
χώρου, κατά τον αιώνα πού ηκολούθησε τον θάνατον του Πυθαγόρου.
, ο κύβος διπλασιάζεται.
Η ανωτέρω μέθοδος, τόσον ευφυής υφ' ην έννοιαν εκτίθεται,
δεν αποδεικνύει μόνον το εφευρετικόν δαιμόνιον του
Αρχύτα και την μεγάλην του οικειότητα με τα σχήματα
του χώρου, άλλα όταν αναλυθή εις τα επί μέρους
βήματα, μας οδηγεί επίσης εις το να εκτιμήσωμεν με ακρίβειαν τας μεγάλας προόδους,
τας οποίας είχεν επιτελέσει εις την Ελλάδα η γεωμετρία του επιπέδου και του
χώρου, κατά τον αιώνα πού ηκολούθησε τον θάνατον του Πυθαγόρου.


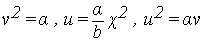

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου