Πυθαγόρας - Πυθαγόριοι

Εγκυκλοπεδικό λεξικό «ΗΛΙΟΥ»

Πυθαγορική αριθμολογία.

Προχωρούντες εις διερευνήσεις περισσότερον αφισταμένας από την εποπτικότητα της Γεωμετρίας οι Πυθαγόρειοι ηδυνήθησαν να θέσουν τας βάσεις της αριθμητικής. Δια των ερευνών των ετέθησαν ζητήματα αναφερόμενα εκ την φύσιν των αριθμών και διεχωρίσθη η καθαρά αριθμητική από την εφηρμοσμένην, ήτις εκλήθη υπό των παλαιών Ελλήνων λογιστική. Περί το τελευταίον τέταρτον του 6ου αιώνος ήρχισαν οι Πυθαγόρειοι τας θεωρητικός των έρευνας. Ανεκάλυψαν ότι τα μήκη των χορδών εξ ων προκύπτουν αρμονικά διαστήματα και ο βαθμός της εντάσεως των έχουν προς άλληλα απλούν ακέραιον λόγον. Επίσης ανεκάλυψαν ότι το ύψος των τόνων είναι ευθέως ανάλογον προς την ταχύτητα της κινήσεως των χορδών και αντιστρόφως ανάλογον προς το μήκος αυτών. Εκ των ανακαλύψεων τούτων αφορμώμενοι, έφθασαν εις το συμπέρασμα ότι, όπως η ουσία των μουσικών τόνων εξαρτάται εκ των αριθμών οι οποίοι καθορίσουν την ποιότητα των και τα διαστήματα των, ούτω και τα λοιπά όντα εις την ουσίαν των είναι αριθμοί. Δεν περιορίζονται να θεωρήσουν οι Πυθαγόρειοι, όπως κάμνομεν ημείς σήμερον, τους αριθμούς ως μέσα δια των οποίων εκτελούμεν λογιστικάς πράξεις, αλλ' απέδωκαν εις αυτούς οντολογκήν σπουδαιότητα. Έκαστος αριθμός εκλαμβάνεται ως οντολογική οντότης, της οποίας πρέπει να αποκαλυφθούν δια της ερεύνης αι ιδιότητες. Δια να ανακαλύψουν τας ιδιότητας ταύτας των αριθμών επρόσεξαν οι Πυθαγόρειοι εις τας αριθμητικάς πράξεις δι' ων σχηματίζονται εξ αλλήλων. Φυσικόν ήτο η έρευνα να δείξη ότι ο διπλασιασμός και η αντιστοιχούσα προς τούτον διαίρεσις δια του 2 είναι αι κατ' εξοχήν γενετικαί των αριθμών πράξεις. Επί τη βάσει της τοιαύτης διαπιστώσεως διήρεσαν τους αριθμούς εις επιδεκτικούς διαιρέσεως δια του 2, τους οποίους κάλεσαν αρτίους, και εις μη επιδεκτικούς, τους οποίους ωνόμασαν περιττούς. Γενικεύοντες δε την εν λόγω αντιστοιχίαν των περιττών και των αρτίων ανήχθησαν εις την μεταξύ του απείρου και πεπερασμένου αντίθεσιν. Προνομιακήν θέσιν εις το σύστημα των Πυθαγορείων κατέχει ο περιττός αριθμός όστις αποτελεί σύνολον με αρχήν, μέσον και τέλος. Ο περιττός ταυτίζεται με το πεπερασμένον, ο άρτιος με το άπειρον, διότι είναι διαιρετός έπ’ άπειρον. Ο άρτιος έχει μέσα εις τον εαυτόν του το άπειρον, εν κενόν, το οποίον επιτρέπει την επ' άπειρον διαίρεσιν.

Προχωρούντες εις την έτη τη βάσει της διαιρετότητας διερεύνησιν των αριθμών διέστειλαν και άλλα είδη. Ως τρίτον είδος ανεγνώρισαν τον αρτιοπέριττον αριθμόν, ήτοι τον αριθμού όστις εις πρώτην διαίρεσιν δίδει αριθμούς περιττούς, όπως ο 6 και ο 10, οίτινες δίδουν το 3 και 5. Τέταρτον είδος αριθμού εθεωρήθη ο περισσάρτιος, ο αναλυόμενος δηλαδή εις άρτιον και περιττόν, όπως ο 12 = 3x4, και πέμπτον είδος τον αρτιάκις άρτιον, όπως ο 32 = 4x8.

Ωθούμενοι αφ' ετέρου της διαιρέσεως και του πολλαπλασιασμού λαμβάνεται υπ' όψιν και η πρόσθεσις δια τον προσδιορισμόν των οντολογικών ιδιοτήτων των αριθμών. Ή δεκάς ως προκύπτουσα εκ της προσθέσεως των τεσσάρων πρώτων κατά σειράν αριθμών 1+2 + 3 + 4 = 10, εκτιμάται ως συγκεντρώνουσα άπαντα τα προσόντα αυτών. Περιέχει όλα τα είδη των αριθμών, διότι το 2 αντιπροσωπεύει τους αρτίους, το 3 τους περιττούς, το 1 το αρτιοπέριττον είδος, διότι γεννά και το περιττόν και το άρτιον, και εν τέλει και το 4, όπερ είναι ο πρώτος τετράγωνος αριθμός. Ο σχηματισμός των αριθμών εξετάζεται υπό των Πυθαγορείων επί τη βάσει του διπλασιασμού και τής προσθέσεως.

Οι αριθμοί αναλύονται εις τους παράγοντας οίτινες τους αποτελούν είτε δια πολλαπλασιασμού είτε δια προσθέσεως. Συγκρίνεται δε το άθροισμα των διαιρετών του αριθμού συμπεριλαμβανομένης και της μονάδος προς τον αριθμόν και επί τη βάσει της συγκρίσεως ταύτης οι αριθμοί διακρίνονται εις υπερτελείς, ελλιπείς και τελείους. Υπερτελής είναι εις αριθμός όταν το άθροισμα των διαιρετών του είναι μεγαλύτερον από αυτόν (π.χ. του 12 μεγαλύτερον ο 1 +2 + 3+4 + 6), ελλιπής είναι όταν το άθροισμα των διαιρετών του υπολείπεται αυτού (π.χ. του 8 μικρότερον του 1 + 2 + 4) . Τέλειος δε είναι ο αριθμός του οποίου το άθροισμα των διαιρετών του είναι ίσον με αυτόν (28 = 1+2 + 4 + 7+14).

Αφ' ετέρου οι Πυθαγόρειοι από την διακρίνουσαν τον ελληνικόν λαόν τάσιν προς την εποπτείαν, εξήτασαν τους αριθμούς από της απόψεως της γεωμετρικής αυτών παραστάσεως. Ο γεωμετρικός των συμβολισμός γίνεται δια γεωμετρικών σχημάτων, εις τα όποια αι μονάδες των αριθμών παρίστανται δια σημείων αποτελούντων γεωμετρικά σχήματα. Κατόπιν τούτου οι αριθμοί χαρακτηρίζονται ως τρίγωνοι, τετράγωνοι, πεντάγωνοι, εξάγωνοι, πυραμιδοειδείς, κύβοι, επίπεδοι κλπ. Τρίγωνος π.χ. είναι ό αριθμός 3. διότι αι τρεις του μονάδες δύνανται να συμβολισθούν δια τριών στιγμών, εκ των οποίων εκάστη κατέχει την κορυφήν γωνίας ισοσκελούς τριγώνου. Δεύτερος κατά σειράν τρίγωνος αριθμός είναι ο 6, ούτινος η διάταξις των μονάδων, συμβολιζομένων δια στιγμών, δύναται να απαρτίση τρίγωνον κατά τον εν τω σχήματι υπ' αριθ. 1 υποδεικνυόμενον τρόπον.

Σχήμα 1

Οι Πυθαγόρειοι εμελέτησαν την γεωμετρικήν παράστασιν των τελείων αριθμών και κατέληξαν εις σημαντικά αποτελέσματα. Λαμβάνοντες ως αφετηρίαν την μονάδα καταρτίζουν σειράς δια της διαδοχικής προσθήκης των περιττών αριθμών, εις τας οποίας το άθροισμα δίδει αριθμόν τέλειον, όστις είναι συγχρόνως και τετράγωνος (δηλαδή παράγεται δια πολλαπλασιασμού αριθμού επί τον εαυτόν του (2X2 = 4, κλπ.)

1

1+3 = 4

1+3 + 5 = 9

1+3+5+7 = 16

1+4+3+5+7+9 = 23.

Γεωμετρικώς παρίστανται οι δια των διαδοχικών προσθέσεων προκύπτοντες αριθμοί δια του γνώμονος. Γνώμων δε είναι η ορθή γωνία την οποίαν εχρησιμοποίουν δια να καθορίζουν παρατηρούντες το μήκος της ριπτομένης υπό της κατακόρυφου πλευράς σκιάς την ώραν της ημέρας. Ομοιάζει με την γωνίαν την οποίαν χρησιμοποιούν οι ξυλουργοί και σήμερον. Η μονάς συμβολίζεται υπό μιας στιγμής σημειούμενης έναντι των ακρών των καθοριζουσών την γωνίαν γραμμών (βλέπε σχήμα 2).

Σχήμα 2

Εάν περιβάλωμεν τον αρχικώς ληφθέντα γνώμονα δια τριών στιγμών συμβολιζουσών τον πρώτον τριγωνικόν αριθμόν (3), τότε τα άθροισμα της μονάδος μετά του 3 θα αποτελέση το πρώτον τετράγωνον, κατά το σχήμα 3.

Σχήμα 3

Εκ του σχήματος τούτου είναι καταφανές ότι ο αριθμός 3 είναι ο πρώτος γνώμων. Δι' ομοίου συμβολισμού προχωρούμεν εις την παράστασιν του 5 ως δευτέρου γνώμονας κλπ., κατά το σχήμα 4.

Σχήμα 4

Δια των διατάξεων των σημείων (του σχήματος 4) εντός γνωμόνων οίτινες εμπερικλείουν αλλήλους, σχηματίζονται διαδοχικώς τετράγωνα, ήτοι 2x2 = 4, 3x3 = 9, 4x4 = 16. Έκαστος άρα των γνωμόνων (3, 5, 7) εμφανίζεται ως διαφορά δύο τετραγώνων, των οποίων ή πλευρά διαφέρει κατά μονάδα. Ως πρός δε τους τελείους αριθμούς, οι Πυθαγόρειοι ανεκάλυψαν ότι ήσαν το άθροισμα της σειράς περιττών αριθμών κατά τον τύπον :

1 + 3 + 5 + 7 ... + + (2 ν—1) = ν.ν

Κατά τον αυτόν τρόπον εξήτασαν και τα αθροίσματα των αρτίων αριθμών, διατεταγμένων εις σειράς αφορμωμένας από του δύο. Εις τον αρχικόν γνώμονα παρενθέτουν δύο στιγμάς (βλέπε σχήμα 5), περιβάλλουν δε τούτον διαδοχικώς δι’ αρτίων αριθμών, (σχήμα 6). Ούτω προκύπτουν αι ακόλουθοι αριθμητικαί σειραί :

2 + 4 = 6 ή (3x2)

2 + 4 + 6=12 ή (3x4)

2 + 4 + 6 + 8 = 20 ή (4x5).

Τα αθροίσματα των είναι άρτιοι αριθμοί, δυνάμενοι να αναλυθούν εις δύο παράγοντας, (Σχήμα 5) εξ ων ο πρώτος ισούται με το ήμισυ του τελευταίου όρου της σειράς, ο δε έτερος με το αυτό ήμισυ ηυξημένον κατά την μονάδα.

Σχήμα 5

Οι αριθμοί ούτοι καλούνται ετερομήκεις και ορίζονται ως «ἔχοντες τὴν ἐτέραν πλευρὰν τῆς ἐτέρας μονάδι μείζονα», ήτοι (ν—1).ν. Οι ετερομήκεις αριθμοί παρίστανται δι' ορθογωνίων εν αντιθέσει προς τους τετραγώνους, οίτινες παρίστανται δια τετραγώνων. Οι Πυθαγόρειοι εθεώρουν τους ετερομήκεις ως εμπερικλείοντας μέσα εις τον εαυτόν των την απειρότητα. Εκτός των τριγώνων αριθμών εγίνετο λόγος εις την αρχαιότητα και περί πενταγώνων, οίτινες διετάσσοντο εις σειράς, της οποίας λύγος των όρων ήτο το 3 (5—2). Ήτοι πεντάγωνοι αριθμοί ήσαν οι αποτελούντες την σειράν : 1, 4, 7, 10.

Σχήμα 6

Η περί αναλογιών θεωρία των Πυθαγορείων.

Σημαντική ανακάλυψις των Πυθαγορείων υπήρξε και η περί αναλογιών διδασκαλία των. Λέγοντες αναλογία οι Πυθαγύρειοι ενόουν «Ομοιότητα λόγων». Οταν δηλαδή δοθούν (ορισμένοι αριθμητικοί όροι και παρατηρηθή ότι η αριθμητική σχέσις η υφισταμένη μεταξύ του πρώτου όρου και του δευτέρου υφίσταται και μεταξύ του δευτέρου και του τρίτου, τότε λέγομεν ότι οι όροι ούτοι αποτελούν αναλογίαν. Οι Πυθαγόρειοι διέκριναν τρία είδη αναλογιών, την άριθμητικήν, την γεωμετρικής και την υπεναντίαν την οποίαν εκάλουν και αρμονικήν. Αριθμητική είναι η αναλογία όταν οι τρεις αριθμητικοί όροι παρουσιάζουν μίαν σταθεράν διαδοχικώς διαφοράν, ήτοι : α—β = β—γ, 6—4 = 4—2. Η διαφορά δηλαδή μεταξύ του πρώτου και του δευτέρου είναι η αυτή με την μεταξύ του δευτέρου και του τρίτου όρου διαφοράν. Εις την αναλογίαν αυτήν το 6:4 μεγαλύτερον του 4:2. Εις την γεωμετρικήν αναλογίαν όν λόγον έχει ο πρώτος όρος προς τον δεύτερον, τον αυτόν έχει ο δεύτερος προς τον τρίτον, ήτοι α:β = β:γ, 8:4 = 4:2. Εις ταύτην ο λόγος των μεγαλυτέρων ορών 8:4 είναι ο αυτός με τον λόγον των μικρότερων 4:2, ήτοι 8:4 = 4:2. Εις την αρμονικήν αναλογίαν η διαφορά ήτις προκύπτει αν αφαιρεθή ο δεύτερος όρος από τον πρώτον αποτελεί κλασματικόν μέρος του πρώτου, ίσον με το κλασματικόν μέρος του τρίτου κατά τον οποίον υπερέχει αυτού ο δεύτερος. Ήτοι αν δοθούν οι αριθμοί 6, 4, 3 η διαφορά 2 ην δίδει ο δεύτερος όρος 4 αφαιρούμενος από τον 6, είναι το 1:3 τούτου. Επίσης και η διαφορά 1 ήτις προκύπτει αφαιρουμένου του 3 από το 4, είναι το 1:3 του τρίτου όρου 3. Την αναλογίαν ταύτην γράφομεν χρησιμοποιούντες κλασματικήν παράστασιν ως εξής : (6 — 4):(4 — 3) = 6:3, και γενικώς (α— β):(β — γ) = α:γ. Εις αυτήν ο λόγος των μειζόνων δέων είναι μεγαλύτερος από τον λόγον των μικρότερων ήτοι 6:4 μεγαλύτερον του 4:3, και γενικώς α:β μεγαλύτερον του β:γ.

Εκ της αναλογίας ταύτης προεχώρησαν οι Πυθαγόρειοι εις την ανακάλυψιν της λεγομένης «μουσικής μεσότητος», ήτις εθεωρήθη η τελειοτέρα πασών, και παριστανωμένη με νεώτερα μαθηματικά σύμβολα εκφράζεται δια της αριθμητικής παραστάσεως: α:[(α + β):2] = [(2αβ):(α+β)]:β.

Ως προς την υπό των αρχαίων παράστασιν των υπενθυμίζομεν ότι δια την αριθμητικών υποδήλωσιν των αρμονιών δεν εχρησιμοποιούντο κλασματικαί παραστάσεις Α:Β = Μ:Ν, αλλά εδηλούντο αύται ως ισοδύναμα γινόμενα Α.Ν = Ε.Μ. Αι εν λόγω ανακαλύψεις εφηρμόσθησαν και εις την μουσικήν, διότι τα μουσικά διαστήματα εθεωρήθη σαν αντιστοιχούντα προς τους αριθμητικούς λόγους τους υφισταμένους μεταξύ των τιμών δια των οποίων καθορίζονται τα μήκη των χορδών, της εντάσεως ούσης της αυτής. Ή οκτάβα (διαπασών) καθωρίσθη ως αντιστοιχούσα εις τον λόγον 2:1, ή πέμπτη (ή δια πέντε) εις τον λόγον 3:2, και η τετάρτη (ή δια τεσσάρων) εις τον λόγον 4:3. Δια δε την παράστασιν των τεσσάρων σταθερών τόνων του οκτάχορδου καθιέρωσαν οι Πυθαγόρειοι τους αριθμούς 6, 8, 9 , 12, εθεώρησαν δε την δια πασών ως εκφραζομένην δια της σχέσεως 12:6, την πέμπτην δια 12:8 και την τετάρτην δια 12:9.

Ως αρμονικόν δε μέσον μεταξύ 6 και 12 εθεωρήθη ο 8, διότι οι αριθμοί 12, 8, 6 αποτελούν αρμονικήν αναλογίαν.

Γεωμετρικαί ανακαλύψεις των Πυθαγορείων.

Σημαντικάς ανακαλύψεις επραγματοποίησαν οι Πυθαγόρειοι εις την γεωμετρίαν. Ανέπτυξαν κυρίως την μετρικήν γεωμετρίαν ασχοληθέντες με την μέτρησιν γεωμετρικών μεγεθών. Αι κυριώτεραι ανακαλύψεις των υπήρξαν αι ακόλουθοι:

1ον) Κατά μαρτυρίαν του Πρόκλου (Σχόλ. εις Εύκλ. Στοιχεία, έκδοσις Φριτλάϊν , σελ. 304, 11).Ο Πυθαγόρας ανεκάλυψεν ότι δοθέντος ενός σημείου ο περί αυτό τόπος διανέμεται εις γωνίας, ων το άθροισμα ισούται με τέσσαρας ορθάς. «Ὁ περὶ ἕν σημεῖον τόπος εἰς τέτρασιν ὀρθαίς ἴσας γωνίας διανέμεται».

O τόπος ούτος πληρούται υπό 6 ισοπλεύρων τριγώνων. Επίσης πληρούται υπό τεσσάρων τετραγώνων και τριών κανονικών εξαγώνων. Εάν όμως προσπαθήσω μεν να πληρώσωμεν αυτόν δι' άλλων πολυγώνων το άθροισμα των γωνιών των θα παρουσίαση η έλλειψιν ή πλεόνασμα εν συγκρίσει προς τας 4 ορθάς. Κατά τον Πρόκλον οι όροι παραβολή, υπερβολή και έλλειψις εισήχθησαν κατά πρώτον υπό των Πυθαγορείων προς σύγκρισιν γεωμετρικών μεγεθών, εχρησιμοποιηθήσαν δε κατόπιν υπό του Απολλωνίου δια την ονομασίαν των γνωστών καμπύλων.

2ον) Εις τους Πυθαγορείους οφείλεται κατά μαρτυρίαν του Πρόκλου και η απόδειξις του θεωρήματος του αποδεικνύοντας ότι το άθροισμα των γωνιών παντός τριγώνου ισούται με δύο ορθάς.

3ον) Υπ' αυτών ελύθη το πρόβλημα το συνιστάμενον εις την κατασκευήν επί δοθείσης ευθείας υπό ωρισμένην γωνίαν παραλληλογράμμου το οποίον να είναι ίσον προς δοθέν τρίγωνον.

4ον) Είχον φθάσει εις την διαίρεσιν των γεωμετρικών σχημάτων και την σύνθεσιν αυτών δια τριγώνων.

5ον) Η παράδοσις αποδίδει εις τους Πυθαγορείους και την εύρεσιν των λεγομένων «κοσμικών σωμάτων», ήτοι των τεσσάρων στοιχείων εξ ων έχει συσταθή το κοσμικόν σύμπαν. Ταύτα είναι το τετράεδρον, όπερ συμβολίζει το πυρ, το οκτάεδρον, όπερ συμβολίζει τον αέρα, το εικοσάεδρον, όπερ συμβολίζει το ύδωρ και τον κύβον, ο όποιος συμβολίζει την γην. Έκτος τούτων είναι λίαν πιθανόν ότι εγνώριζον και το πεντάεδρον. Τούτο το εικάζομεν εξ ειδήσεων αίτινες αναφέρουν ότι οι Πυθαγόρειοι εχρησιμοποίουν το πεντέγραμμα (κοινώς σήμερον πεντάλφα) ως σύμβολον υγείας. Λέγοντες οι Πυθαγόρειοι κανονικά σώματα ενόουν σώματα των οποίων η επιφάνεια σχηματίζεται υπό τετραγώνων και ισοπλεύρων τριγώνων το απλούτατον εκ τούτων ήτο ο κύβος, όστις σύγκειται από εξ τετράγωνα τεμνόμενα κατ' ορθάς γωνίας. Το τετράεδρον είναι η τετράπλευρος πυραμίς, ήτις σχηματίζεται από τέσσαρα ισόπλευρα τρίγωνα. Το οκτάεδρον σχηματίζεται από οχτώ ισόπλευρα τρίγωνα, το δε εικοσάεδρον από είκοσι. Εις τα τέσσαρα ταύτα σώματα προστίθεται ως πέμπτον και το δωδεκάεδρον, το οποίον κατεσκευάσθη, ως αναφέρει η παράδοσις. υπό του Ιππάσου κατά το πρώτον τέταρτον του πέμπτου αιώνος. Τούτο το εθεώρουν σχιματιζόμενον υπό δώδεκα ισοπλεύρων πενταγώνων, κατά δε τον Πλούταρχον ήτο σύμβολον «τῆς τοῦ παντὸς σφαῖρας». Εις εν απόσπασμα του Φιλολάου αναγινώσκομεν : «Καὶ τὰ μὲν τῆς σφαῖρας σώματα πέντε ἐστί, τὰ ἐν τῇ σφαῖρα πῦρ (καὶ) ὕδωρ καὶ γῆ καὶ ἀήρ, καὶ ὅ τᾶς σφαίρας ὁλκάς πέμπτον». (Τα σώματα (τα ενυπάρχοντα εις το εσωτερικόν) της σφαίρας είναι πέντε, πυρ και ύδωρ και γη και αήρ και εκείνο το οποίον χρησιμεύει ως φορτηγόν πλοίον της σφαίρας, το πέμπτον). Το πέμπτον σώμα κοινώς θωρείται ως εγγεγραμμένον εις την σφαίραν δωδεκάεδρον.

Την παράδοσιν ότι ο Ίππασος κατώρθωσε να εγγράψη εις σφαίραν το δωδεκάεδρον μας διέσωσεν ο Ιάμβλιχος. όστις εις τον υπ' αυτού συγγραφέντα βίον του Πυθαγόρα (88 κ.ε.) γράφει τα ακόλουθα : «Περὶ δε Ἱππάσου μάλιστα (δηλ. φάσιν) ὡς ἦν μὲν τῶν Πυθαγορείων, διὰ δὲ τὸ ἐξενεγκεῖν καὶ γράψασθαι πρῶτος σφαῖραν τὴν ἐκ τῶν δώδεκα πενταγώνων ἀπώλετο κατά θάλασσαν ὡς ἀσεβήσας δόξαν δὲ λαβοί ὡς εὑρών, εἶναι δὲ πάντα ἐκείνου τοῦ ἀνδρός προσαγορεύουσι γὰρ οὕτω τὸν Πυθαγόραν καὶ οὐ καλοῦσιν ὀνόματι». «Περί δε του Ιππάσου ακριβώς λέγουν ότι συγκατελέγετο εις τους Πυθαγορείους. Επειδή δε εδημοσίευσε πρώτος και δια γραφικής παραστάσεως παρέστησε την σφαίραν την αποτελουμένην εκ δώδεκα πενταγώνων εύρε τον θάνατον πνιγείς εις την θάλασσαν επειδή (δια των αποκαλύψεων του) διέπραξεν ασέβεια. Έλαβε δε την δόξαν ότι αυτός έκαμε (την ανωτέρω μνημονευθείσαν) ανακάλυψιν, ενώ όλα αυτά ήσαν ευρήματα «εκείνου του ανδρός» διότι δι' αυτής της προσαγορεύσεως συνηθίζουν να ονομάζουν τον Πυθαγόραν και δεν τον ονομάζουν με το όνονομά του.

Εις το χωρίον τούτο η «ἐκ δώδεκα πενταγώνων σφαῖρα» είναι το εκ δώδεκα πενταγώνων δωδεκάεδρον, όπερ λόγω του ότι προσεγγίζει προς την σφαίραν, εκαλείτο κοινώς παρά τοις αρχαίοις σφαίρα. Ως προς τας ειδήσεις ταύτας εγένοντο εις τους νεωτέρους ιστορικούς πολλοί συζητήσεις. Η έρευνα μετά επίμονον αντιβολήν των ειδήσεων κατέληξεν εις το συμπέρασμα ότι οι Πυθαγόρειοι εγνώριζον εμπειρικώς την ύπαρξιν των πέντε τούτων κανονικών σωμάτων ουχί όμως και την γεωμετρικήν των κατασκευήν. Δια να συντελεσθή η κατά γεωμετρικούς κανόνας κατασκευή των σωμάτων τούτων χρειάζονται να λυθούν προβλήματα αναφερόμενα εις τα ασύμμετρα μεγέθη. Τοιαύτα όμως προβλήματα εμελετήθησαν και ελύθησαν μόνον κατά το πρώτον ήμισυ του τετάρτου αιώνος υπό του Αθηναίου μαθηματικού Θεατήτου, ως θα ίδωμεν κατωτέρω. Συνεπώς η ερευνά κατέληξαν εις το συμπέρασμα ότι οι Πυθαγόρειοι γνωρίζον μόνον εκ της εμπειρίας τα εν λόγω σχήματα. Αρχαιολογικοί ερευνά έδειξαν ότι εις την βόρειον Ιταλίαν κατά τον έκτον π. Χ. αιώνα ήσαν γνωστά στερεά με δώδεκα έδρας. Πλησίον της Παδούης ευρέθη εν χαλκούν δωδεκάεδρον και 26 αντικείμενα δωδεκαεδρικής μορφής. Οι κάτοικοι της βορείου Ιταλίας κατεσκεύαζον τοιαύτα αντικείμενα απομιμούμενοι την κρυσταλλικήν μορφήν υπό την οποίαν εμφανίζεται εις τα μέρη εκείνα ο πυρίτης. Τοιαύτα αντικείμενα έδωσαν αφορμήν να σχηματίσουν και οι Πυθαγόρειοι εμπειρικήν εποπτείαν περί δωδεκαέδρου και εικοσιέδρου, εφ' όσον απαντώνται και κρυσταλλώσεις εν τη φύσει με είκοσι έδρας. Ο κατόπιν ευρύτατα διαδοθείς Νεοπυθαγορισμός απέδωκεν εις τους Πυθαγορείους αναδρομικώς και την γνώσιν της γεωμετρικής κατασκευής των πέντε γεωμετρικών σωμάτων. Συμφώνως προς τα ανωτέρω, το παρατεθέν ανωτέρω απόσπασμα του Φιλολάου λαμβάνει άλλην ερμηνείαν. Τα σώματα άτινα αναφέρονται ως ενυπάρχοντα εις την σφαίραν δεν είναι τα κοσμικά σώματα, ή δε ολκάς δεν είναι το δωδεκάεδρον. Ό Φιλόλαος αναφέρεται εις την θεωρίαν του Εμπεδοκλέους, όστις εδέχετο ότι τα τέσσαρα στοιχεία περιέχονται μέσα εις την σφαίραν.

6ον) Υπό των Πυθαγορείων ετέθη το πρόβλημα της κατασκευής σχήματος το όποιον να είναι ίσον με εν άλλο δοθέν σχήμα και όμοιον προς έτερον επίσης δοθέν.

Άλλ' η ανακάλυψις εκείνη, ήτις επέδρασε τα μέγιστα δια την περαιτέρω εξέλιξιν της γεωμετρίας, είναι η απόδειξις της προτάσεως ήτις λέγει ότι το τετράγωνον της υποτεινούσης του ορθογωνίου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο καθέτων πλευρών αυτού. Η πρότασις αύτη επωνομάσθη «Πυθαγόρειον θεώρημα» και η ανακάλυψης απεδόθη εις τον Πυθαγόραν όστις ευχαριστών τους θεούς, λέγεται ότι προσέφερεν εις αυτούς εκατόμβην. Η προσφορά αιματηράς θυσίας υπό των Πυθαγορείων είναι όλως απίθανος. Επίσης δεν δυνάμεθα να γνωρίζωμεν κατά ποίον τρόπον απεδείχθη κατά την εποχήν εκείνην το θεώρημα. Ούτε είναι βέβαιον ότι οφείλεσαι αύτη εις τον Πυθαγόραν. Είναι βέβαιον ότι οι Αιγύπτιοι και οι Βαβυλώνιοι εγνώριζον ότι εν τρίγωνον του οποίου αι πλευραί έχουν την σχέσιν των αριθμών 3, 4 και 5, είναι ορθογώνιον. Αλλά το ζήτημα δεν αναφέρεται εις την εμπειρικήν διαπίστωσιν της υπάρξεως τοιαύτης μεταξύ των πλευρών σχέσεως, αλλ' εις την απόδειξιν της κατά γενικόν τρόπον διατυπωθείσης προτάσεως. Οι νεώτεροι μαθηματικό έχουν υποδείξει 12 τρόπους, κατά τους οποίους είναι δυνατόν να επιτευχθή ή λύσις. Δεν είναι απίθανον οι Πυθαγόρειοι να ανεκάλυψαν την απόδειξιν μελετώντες τας ιδιότητας των τετραγώνων αριθμών.

Εξ ίσου πιθανόν είναι ότι επισημοποίησαν τας σχέσεις των αναλογιών, τας υφιστάμενος μεταξύ των πλευρών ομοίων τριγώνων, αίτινες ήσαν ήδη γνωσταί εις τον Θαλήν. Εκτός τούτου, επί τη βάσει της αυτής αρχής των αναλογιών, ηδυνήθησαν οι Πυθαγόρειοι να κατασκευάσουν τετράγωνον, όπερ έχει εμβαδόν ίσον με το δοθέν ορθογώνιον. Διότι εν τω δοθέντι ορθογωνίω τριγώνω ΑΒΓ (σχήμα 7) η εκ της κορυφής της ορθής γωνίας αγομένη ΑΔ, λαμβανομένη εις το τετράγωνον, ισούται με το γινόμενον των ΒΔ και ΔΓ. Άρα δυνάμεθα, εάν κατασκευάσωμεν τετράγωνον, του οποίου η πλευρά είναι ίση με την ΑΔ, τούτο θα έχει εμβαδόν ίσον με το εμβαδόν ορθογωνίου παραλληλογράμμου.

Σχήμα 7

Η βάσις και το ύψος είναι η ΒΔ και η ΔΓ. Ούτω επετεύχθη ο τετραγωνισμός του ορθογωνίου και με αυτόν ετέθη το πρόβλημα του τετραγωνισμού και άλλων σχημάτων.

Η ανακάλυψις των ασύμμετρων μεγεθών.

Οι Πυθαγόρειοι εθεώρουν το τετράγωνον ως το θεμελιωδέστερον και απλούστερον των ευθυγράμμων σχημάτων. Από απόψεως μετρητικής επόμενον ήτο να δεχθούν ως αφετηρίαν τετράγωνον, του οποίου η πλευρά λαμβάνεται ίση με την μονάδα

Σχήμα 8

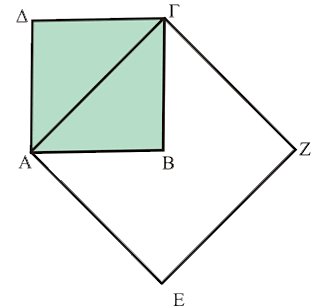
θεωρουμένην ως αρχικόν μέτρων. Έστω το τετράγωνον ΑΒΓΔ (σχήμα 8) του οποίου την πλευράν λαμβάνομεν ίσην με την μονάδα. Αν θελήσωμεν να κατασκευάσωμεν τετράγωνον με εμβαδόν διπλάσιον του δοθέντος, ο ζητούμενος διπλασιασμός δεν δύναται να επιτευχθή δια του διπλασιασμού της πλευράς, διότι αν λάβωμεν πλευράν έχουσαν τιμήν 2 και σχηματίσωμεν τετράγωνον, το εμβαδόν θα τετραπλασιασθή (2X2 = 4). Το Πυθαγόρειο θεώρημα όμως μας δίδει αμέσως την δυνατότητα να λύσωμεν γεωμετρικώς το τεθέν πρόβλημα. Επιζευγνύοντες τα σημεία Α και Γ του προς διπλασιασμόν δοθέντος τετραγώνου ΑΒΓΔ (σχήμα 9) σχηματίζομεν την διαγώνιον ΑΓ,

Σχήμα 9

ήτις είναι συγχρόνως και υποτείνουσα των ορθογωνίων τριγώνων ΑΒΓ και ΑΔΓ. Αν με πλευράν την ΑΓ σχηματίσωμεν το τετράγωνο» ΑΕΖΓ, το εμβαδόν αυτού προφανώς θα είναι διπλάσιον άπα το εμβαδόν του δοθέντος τετραγώνου ΑΒΓΔ, διότι κατά το Πυθαγόρειον θεώρημα, το τετράγωνον της υποτεινούσης (ΑΓ) ισούται τω αθροίσματι των τετραγώνων των δύο άλλων πλευρών (της ΑΒ και της ΒΓ). Δια της χρησιμοποιήσεως της διαγωνίου, το πρόβλημα από γεωμετρικής απόψεως ελύθη. Αν όμως θελήσωμεν να προσδιορίσωμεν αριθμητικώς την τιμήν της διαγωνίου ταύτης, θα προσκόψωμεν εις ανυπέρβλητους δυσχερείας. Τίθεται λοιπόν δυσχερέστατον πρόβλημα, όπερ θα ηδύνατο δια φραστικής διατυπώσεως, πλησιαζούσης το περιεχόμενον του Πυθαγορείου θεωρήματος, να εκφρασθή δια του ακολούθου ερωτήματος: Ποίον είναι το μήκος της υποτεινούσης του ορθογωνίου τριγώνου, όταν εκάστη των καθέτων πλευρών του ισούται με την μονάδα; Η λύσις ανεζητήθη δια της ευρέσεως κλασματικής αριθμητικής εκφράσεως, ήτις, πολλαπλασιαζόμενη με τον εαυτόν της, να δίδη τον αριθμόν 2. Ήτοι, ετέθη το πρόβλημα της ευρέσεως της τετραγωνικής ρίζης του 2. Μετά πολλάς αναζητήσεις, οι Πυθαγόρειοι κατέληξαν εις το συμπέρασμα άτι το ζητούμενον μέγεθος τυγχάνει ασύμμετρον προς την πλευράν, τούτο σημαίνει άτι δεν δύναται να ύπαρξη εν κοινόν μέτρον, το όποιον να μετρά την διαγώνιον και την πλευράν. Διότι εάν ήσαν αριθμοί σύμμετροι, ο λόγος αυτών θα εξεφράζετο δια του ανάγωγου κλάσματος δ:π, εις το όποιον το π συμβολίζει την πλευράν. το δε δ την διαγώνιον. Τους αριθμούς π και δ λαμβάνομεν ως τους κατά την αριθμητικήν τιμήν ελαχίστους και μη επιδεχόμενους αναγωγήν, εις μικρότερους. Αλλά κατά το Πυθαγόρειον θεώρημα το δ.δ = 2π.π. Τούτο όμως σημαίνει ότι το 2π.π είναι αριθμός άρτιος, εκ τούτου δε έπεται ότι και ο δδ είναι αριθμός άρτιος. Άρα και ο αριθμός δ είναι άρτιος. Επειδή όμως το δ:π κλάσμα ελήφθη ανάγωγον. πρέπει ο αριθμός π να είναι περιττός. Εφ' όσον όμως ο δ είναι άρτιος, δυνάμεθα το Πυθαγόρειον θεώρημα να το εκφράσωμεν υπό την μορφήν 4(δ:2).(δ:2) = 2π.π η 2.(δ:2).(δ:2) =π.π. Αλλ' είναι φανερόν ότι κατά την παράστασιν ταύτην, ο π, αν εδέχθημεν ως περιττόν, είναι συγχρόνως και άρτιος. Κατά ταύτα η υπόθεσίς μας, κατά την οποίαν το π ελήφθη ως σύμμετρος και δυνάμενος να έχη συμμετρικόν λόγον προς την πλευράν, εκφραζόμενον δια δ:π τυγχάνει ψευδής. Μίαν τοιαύτην δια της εις άτοπον απαγωγής απόδειξιν, φρονεί ο Γάλλος φιλόσοφος Λεόν Μπρούνσβικ ότι είχεν υπ' όψιν του ο Αριστοτέλης όταν γράφη εις τα «Αναλυτικά Πρότερα» (41 α 26) τα ακόλουθα:

«ἀσύμμετρος ἡ διάμετρος διὰ τὸ γίνεσθαι τὰ περιττὰ ἴσα τοῖς ἀρτίοις συμμέτρου τεθείσης. τὸ μὲν οὖν ἴσα γίνεσθαι τὰ περιττὰ τοῖς ἀρτίοις συλλογίζεται, τὸ δ᾽ ἀσύμμετρον εἶναι τὴν διάμετρον ἐξ ὑποθέσεως δείκνυσιν, ἐπεὶ ψεῦδος συμβαίνει διὰ τὴν ἀντίφασιν. τοῦτο γὰρ ἦν τὸ διὰ τοῦ ἀδυνάτου συλλογίσασθαι, τὸ δεῖξαί τι ἀδύνατον διὰ τὴν ἐξ ἀρχῆς ὑπόθεσιν.» σε μοτονικό: «Ασύμμετρος η διάμετρος δια το γίνεσθαι τα περιττά ίσα τοις αρτίοις συμμέτρου τεθείσης. Το μεν ούν ίσα γίνεσθαι τα περιττά τοίς αρτίοις συλλογίζεσθαι, το δ’ ασύμμετρον είναι την διάμετρον εξ’ υποθέσεως δείκνυσιν, επει ψεύδος συμβαίνει δια την αντίφασιν. Τούτο γαρ ήν το διά του αδυνάτου συλλογίζεσθαι, το δείξαι τι αδύνατον διά την αρχής υπόθεσιν.»

(Η διάμετρος είναι ασύμμετρος διότι αν την δεχθώμεν ως σύμμετρον, θα φθάσωμεν εις ισότητα, ήτις θα εξισώνη ένα περιττόν αριθμόν προς ένα άρτιον). Ο Αριστοτέλης θέλει να είπη ότι, αν δεχθώμεν την διαγώνιον του ζητουμένου διπλασίου τετραγώνου ως αριθμόν σύμμετρον, θα αναγκασθώμεν να δεχθώμεν ότι η πλευρά είναι συγχρόνως αριθμός περιττός και άρτιος.

Δια των ερευνών τούτων διεπιστώθη ότι δεν είναι δυνατό να ευρεθή εις αριθμός μετρούμενος υπό αρχικώς ωρισμένη μονάδος μετρήσεως, ο όποιος να αντίστοιχη προς την διαγώνιον τετραγώνου το όποιον έχει πλευράν την μονάδα. Δια να εκφρασθώμεν με νεωτέρους όρους λέγομεν ότι ανεκαλύφθη τότε ότι η τετραγωνική ρίζα του 2 είναι αριθμός ασύμμετρος. Εκείνο το οποίον εθεωρήθη παράδοξον και ανεξήγητον ήτο ότι υπάρχουν εις την πραγματικότητα δεδομένα γεωμετρικά μεγέθη, τα οποία παρ' όλον ότι είναι εποπτικώς αντιληπτά δεν δύνανται να μετρηθούν, αρνούμενα να υποταχθούν εις τον λογισμόν. Ενώ οι Πυθαγόρειοι ισχυρίζονται ότι τα πάντα είναι αριθμοί, ότι εις οιονδήποτε ον αντίστοιχεί αριθμός, ευρέθη ότι μεγέθη τινά αρνούνται να υποταχθούν εις τον οντολογικόν τούτον νόμον. Ώστε δεν είναι το παν αριθμητόν και υποτεταγμένον εις τον λόγον, «ρητόν». Εις την διδομένην πραγματικότητα κάμνει την εμφάνισίν του το άλογον και το άρρητον διασπών και διαταράσσον τας αρμόνικας σχέσεις. Μία τοιαύτη ανακάλυψις δεν ήτο δυνατόν να μη επιφέρη κλονισμόν εις το οικοδόμημα όπερ προσεπάθουν να ανεγείρουν οι Πυθαγόρειοι. Η ανακάλυψις της υπάρξεως ασύμμετρων μεγεθών φυσικόν ήτο να προξενήση κατάπληξιν εις τους κύκλους των Πυθαγορείων, απήχησιν δε ταύτης μας δίδει σχόλιον εις το δέκατον βιβλίον των «Στοιχείων» του Ευκλείδου, έχον ως εξής:

«Τῶν γὰρ Πυθαγορείων λόγος τὸν πρῶτον τὴν περὶ τούτων (δηλαδή τῶν ἀλόγων) θεωρίαν εἰς τοὐμφανές έξαγαγόντα ναυαγίω περιπεσεῖν, καὶ ἴσως ἠνίττοντο, ὅτι πᾶν τὸ ἄλογον έν τῷ παντὶ καὶ ἄλογον καὶ ἀνείδεον κρύπτεσθαι φιλεῖ καὶ εἴ τις ἄν ψυχή τύχη ἐπιδράμοι τῷ τοιούτω εἴδει τῆς ζωῆς καὶ πρόχειρον καὶ φανερὸν τοῦτο ποιήσηται εἰς τὸν τῆς γενέσεως ὑποφέρεται ποντον καὶ τοῖς ἀστάτοις ταύτης κλύζεται ρεύμασιν. τοιοῦτον σέβας καὶ οὗτοι εἶχον οι ἄνδρες περὶ τὴν τῶν ἀλόγων θεωρίαν»

(Διότι λέγουν οι Πυθαγόρειοι ότι ο πρώτος όστις έφερεν εις το φως της δημοσιότητος την περί των ασύμμετρων θεωρίαν, περιέπεσεν εις ναυάγιον και ίσως ήθελον δι' αινιγματικής εκφράσεως να είπουν δια της διηγήσεως αυτής, ότι πάν ό,τι μέσα εις το σύμπαν δεν υποτάσσεται εις τον λόγον, συνηθίζει να αποκρύπτεται και να μένη έξω από την αναλογικήν σχέσιν και την ανάληψιν είδους (δηλαδή καθωρισμένης μορφής). Και εάν καμμία ψυχή ήθελε κατά τύχην ορμήσει προς εν τοιούτον είδος ζωής και ήθελε παρουσιάσει εις το φως της ημέρας το άλογον ,αύτη η ψυχή κατακρημνίζεται εις την υγράν περιοχήν της γενέσεως και κλυδωνίζεται από τα ασταμάτητα της ρεύματα. Τοιούτον σέβας και αυτοί οι άνδρες είχον σχετικώς με την εις τα άλογα (ασύμμετρα μεγέθη) αναφερομένην θεωρίαν). Η έκφρασις «κρύπτεσθαι φιλεῖ» προέρχεται από απόσπασμα του Ηρακλείτου. όστις διαττείνεται ότι εν τη φύσει ενυπάρχει ριζική τις τάσις προς απόκρυψιν. Το άλογον συνεπώς εμφανίζεται εις το ανωτέρω χωρίον ως συμβόλιζαν την φύσιν, ήτις αρνήται να αποκάλυψη εις τον άνθρωπον τα μυστικά της και τιμωρεί ως ασέβειαν την προσπάθειαν να υποβληθή εις τον ζυγόν του λόγου, εκείνο το όποιον λόγω της φύσεως του δεν υποτάσσεται εις το είδος και τον λογικόν καθορισμόν.

Αι συνέπειαι της ανακαλύψεως των ασύμμετρων μεγεθών.

Μετά την ανακάλυψιν ότι υπάρχουν ασύμμετρα γεωμετρικά μεγέθη, οι Πυθαγόρειοι κατενόησαν ότι δεν ήτο δυνατόν να προχωρήσουν εις τας γεωμετρικάς των ερεύνας, χρησιμοποιούντες ακεραίους αριθμούς. Ηναγκάσθησαν να δώσουν εις την άλγεβραν γεωμετρικήν μορφήν. Την εξίσωσιν (α+β). (α+β) =α.α+2βα+β.β την έδειξαν εποπτικώς δια του κατωτέρω σχήματος (Σχ. 10), σχηματίζοντες τετράγωνον, του οποίου η πλευρά είναι το άθροισμα των μηκών α και β και αναλύοντες τούτο εις τετράγωνα και ορθογώνια. Εκ της ανα­λύσεως του τετραγώνου είναι φανερόν ότι εν τω συνόλω του αποτελείται από εν τετράγωνον έχον πλευράν την α. εν τε­τράγωνον έχον πλευράν την β και δύο ορθογώνια έκαστον εκ των οποίων έχει ως διαστάσεις του την α και β, ήτοι (α+β).(α+β) = αα + 2βα + β.β. Είναι επίσης φανερόν ότι η διαφορά του (α+β) · (α+β) και (α·α) είναι το εν είδει γνώμο­νος σχήμα το συναπάρτιζαμενον εκ 2βα+β-β (ήτοι εκ του μικρού τετραγώνου του έχοντος πλευράν β και εκ δυο ορθογωνίων εκατέρου των οποίων η βάσις είναι η α, ύψος δε η β). Ούτω εδημιουργήθη εν είδος γε­ωμετρικής άλγεβρας δια της οποίας εκτελείται πρόσθεσις και αφαίρεσις παριστανομένων των ποσοτήτων δια γραμμών και τετραγώνων και ορθογωνίων επιφανειών. Το γινόμενον του πολλαπλασιασμού παρίσταται δι’ ορθογωνίου του ο­ποίου το ύψος και η βάσις παριστούν τους παράγοντας. Η κατασκευή εν δοθείση επιφάνεια σχημάτων προς λύσιν δοθέντος προβλήματος καλείται διαίρεσις, δύναται δε να παραβληθή με την ομώνυμον αριθμητικήν πράξιν. Κατά τας συγ­κρίσεις ταύτας των γραμμών και επιφανειών εχρησιμοποιήθησαν, ως φαίνεται εξ αξιόπιστων μαρτυριών ήδη υπό των Πυθαγορείων οι όροι παραβολή, υπερβολή και έλλειψις. Ο Πρόκλος, αρυόμενος τας πληροφορίας του από το Εύδημον, γράφει σχετικώς (Σχόλ. εις Ευκλ.. 419) «Ἔστι μὲν ἀρχαῖα φασὶν οἱ περὶ τὸν Εὔδημον καὶ τῆς τῶν Πυθαγορείων Μούσης εὑρήματα ἥ τε παραβολή τῶν χωρίων καὶ ἡ ὑπερβολή καὶ ἡ ἔλλειψις. Ἀπὸ δὲ τούτων καὶ οἱ νεώτεροι τὰ ὀνόματα λαβόντες μετήγαγον αύτὰ καὶ ἐπί τὰς κωνικάς λεγομένας γραμμάς».

Σχήμα 10

Η συμβολή των Πυθαγορείων.

Δια των ερευνών των Πυθαγορείων συμπεριελήφθησαν εις συστηματικήν ενότητα αι μαθηματικαί ανακαλύψεις και συναπετέλεσαν μεθεδικώς συντεταγμένον σύστημα δυνάμενον να μεταδοθή δια της διδασκαλίας και εις τους μεταγενεστέρους. Δια τούτο ωνομάσθησαν αι άνακαλυφθείσαι προτάσεις «μαθήματα», ήτοι αλήθειαι τας όποιας δύναται να προσοικειωδή ο αρχάριος δια της μαθήσεως. Η λέξις μάθησις δεν σημαίνει απλώς κατοχήν του διδασκομένου, άλλα συγχρόνως και βαθείαν τούτου κατανόησιν. Και από μεθοδολογικής απόψεως έθεσαν οι Πυθαγόρειοι τα πρώτα θεμέλια τής μαθηματικής επιστήμης. Ύψωσαν την απόδειξιν εις αυστηρώς λογικήν διαδικασίαν και εχρησιμοποίησαν και την εις άτοπον απαγωγήν, ως αποδεικτικήν μέθοδον. Καθόρισαν την έννοιαν των ακεραίων αριθμών ως συστημάτων απαρτιζόμενων εκ μονάδων και την έννοιαν τής μεταξύ αυτών σχέσεως. Αι προσπάθειαί των να καθορίσουν αριθμητικώς την τετραγωνικήν ρίζαν του 2 εγένοντο αφορμή να λάβουν εντονοτέραν συνείδησιν περί κλασματικών αριθμών. Σπουδαιοτάτη υπήρξεν ώς είδομεν, η ανακάλυψις των ασύμμετρων μεγεθών ήτις έθεσεν αυτούς προ νέων προβλημάτων και προεκάλεσεν έντονον κρίσιν εις την περιοχήν των μαθηματικών σπουδών. Εις την στερεομετρίαν δεν φαίνεται έπιτελέσαντες μεγάλας ανακαλύψεις. Ως προς τας μεταφυσικάς περί τών αριθμών γνώσεις αυτών θα γίνη λόγος εις τό οικείον περί ελληνικής φιλοσοφίας τμήμα.